geometric projection

A projection is an idempotent linear transformation that decomposes vectors onto orthogonal components.

In ML, "projection" often means learned linear transformation, not geometric projection.

Vector decomposition via projection

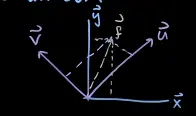
Any vector $\mathbf{v}$ can be decomposed relative to a direction $\mathbf{u}$:

$$\mathbf{v}={\mathbf{v}}_{\parallel }+{\mathbf{v}}_{\perp }$$

where ${\mathbf{v}}_{\parallel }$ points along $\mathbf{u}$ and ${\mathbf{v}}_{\perp }$ is orthogonal to it.

The projection ${\mathbf{v}}_{\parallel }={\text{proj}}_{\mathbf{u}}(\mathbf{v})$ is the foot of the perpendicular from $\mathbf{v}$ to $\text{span}\{\mathbf{u}\}$. The perpendicular component is:

$${\mathbf{v}}_{\perp }=\mathbf{v}-{\mathbf{v}}_{\parallel }$$

The inner product $⟨\mathbf{v},\mathbf{u}⟩$ measures how much $\mathbf{v}$ points along $\mathbf{u}$. Scaling by $1/\Vert \mathbf{u}{\Vert }^2$ gives the right coefficient:

$${\text{proj}}_{\mathbf{u}}(\mathbf{v})=\frac{⟨\mathbf{v},\mathbf{u}⟩}{\Vert \mathbf{u}{\Vert }^2}\mathbf{u}$$

If $\mathbf{u}$ is already a unit vector, this simplifies:

$${\text{proj}}_{\hat{\mathbf{u}}}(\mathbf{v})=⟨\mathbf{v},\hat{\mathbf{u}}⟩\hat{\mathbf{u}}$$

---

For orthogonal basis vectors, any vector decomposes into projections onto each basis direction. Same vector $\mathbf{v}$ in different bases $\{{\mathbf{b}}_1,{\mathbf{b}}_2\}$ or $\{{\mathbf{c}}_1,{\mathbf{c}}_2\}$:

$$\mathbf{v}=\frac{⟨\mathbf{v},{\mathbf{b}}_1⟩}{\Vert {\mathbf{b}}_1{\Vert }^2}{\mathbf{b}}_1+\frac{⟨\mathbf{v},{\mathbf{b}}_2⟩}{\Vert {\mathbf{b}}_2{\Vert }^2}{\mathbf{b}}_2\mathbf{v}=\frac{⟨\mathbf{v},{\mathbf{c}}_1⟩}{\Vert {\mathbf{c}}_1{\Vert }^2}{\mathbf{c}}_1+\frac{⟨\mathbf{v},{\mathbf{c}}_2⟩}{\Vert {\mathbf{c}}_2{\Vert }^2}{\mathbf{c}}_2$$

Each coefficient tells you how much of that basis vector appears in $\mathbf{v}$.

The relation to the cosine and many of the dot product's properties become clear geometrically

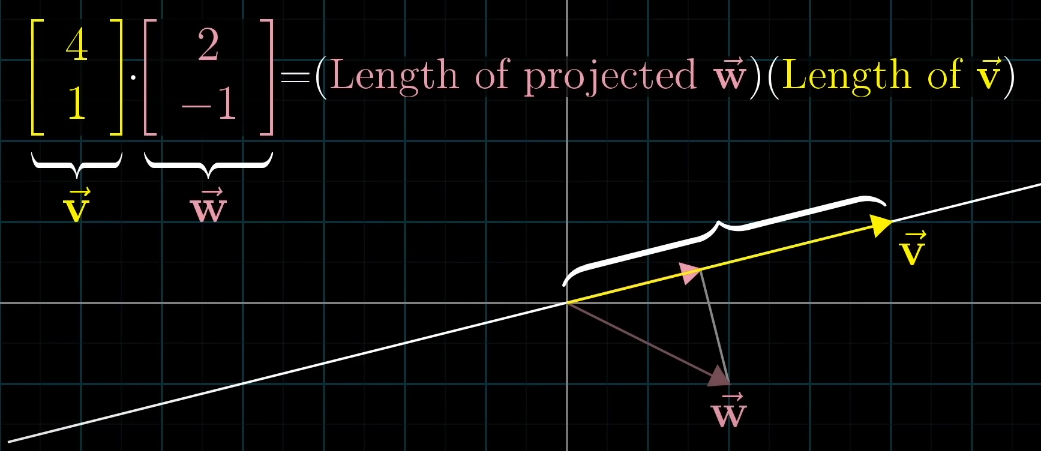
Project one vector onto another and multiply the length of the other with the resulting vector.
The head of the projected vector follows from drawing an orthogonal line from the head of one vector to another.
→ For two vectors on the unit circle, this projection is the cosine of the angle between them.
→ Order does not matter.

Dot product is positive if they point into the same direction, negative for opposing directions:

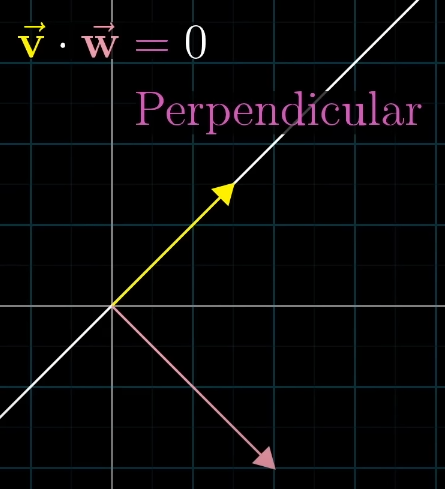
The projected vector $\vec{w}$ has length $0$ if the vectors are perpendicular:

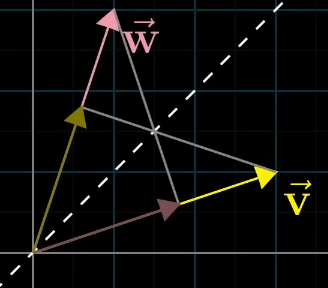
Indifference of order:

Scaling one of those vectors by 2 → dot product is exactly 2x bigger:

$$(2\vec{v})\cdot \vec{w}=2(\vec{v}\cdot \vec{w})$$

Link to original