inner product

Inner Product on a vector space

An inner product $⟨\cdot ,\cdot ⟩$ on a vector space $V$ is a binary operator that takes two vectors and returns a scalar, satisfying the following properties for all $u,v,w\in V$ and all scalars $c\in \mathbb{R}$:
Linearity in the first argument: $⟨au+bv,w⟩=a⟨u,w⟩+b⟨v,w⟩$ for all $a,b\in \mathbb{R}$.
Conjugate symmetry: $⟨u,v⟩=\overline{⟨v,u⟩}$ (for real vector spaces, this simplifies to $⟨u,v⟩=⟨v,u⟩$).
Positive-definiteness: $⟨v,v⟩\ge 0$ with equality if and only if $v=0$.

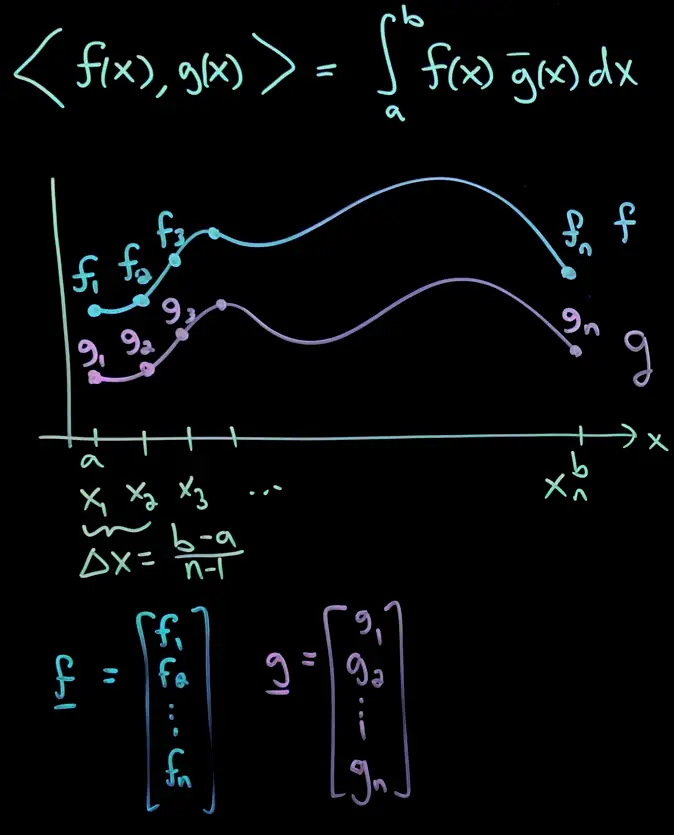
Inner Product of two functions

For two functions on the interval $[a,b]$, the $L^2$ inner product is defined as:

$$⟨f,g⟩={\int }_a^{b}f(x)\overline{g(x)}dx$$

It has all the same properties as any inner product, and tells you how aligned two functions are.
The bar denotes the complex conjugate, so $⟨f,f⟩={\int }_a^b|f(x){|}^{2}dx\ge 0$ (positive definiteness).
For real-valued functions, the bar can be omitted.

This can be thought of taking the dot product of two vectors with infinitely many components, one at each $x$ in the interval, or rather it is just the Riemann approximation: $⟨f,g⟩={\lim }_{n\to \infty }{\sum }_{i}f(x_i)\overline{g(x_i)}\Delta x$.

https://en.wikipedia.org/wiki/Inner_product_space

${\mathbb{R}}^{1\times n}\times {\mathbb{R}}^{n{\times }_1}=\mathbb{R}$

positive definite