platonic space

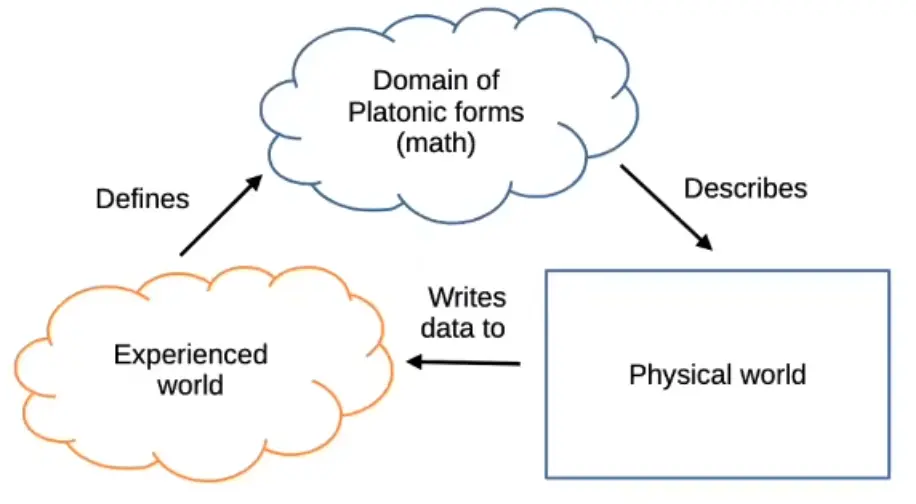
Joscha Bach’s reinterpretation of Plato’s idealism:

Plato was not actually an idealist in the sense that he believed that conscious or mental experience is primary.

Plato takes these ideal forms as starting points. The ideal table is sometimes given as an example, but that’s probably not a core arcchetype of the universe or of god itself, but tables are created by human beings in particular cultural contexts, and they are an archetype in our perception. The way in which we classify the world, there is something like an ideal table. The forms that Plato is talking about are actually dimensions in an embedding space. In some of his texts, he alludes to a world outside of our perception, our mental construction that we experience, and that world is an outside [of our?] simulated world that is isomorphic to the world that we experience in these forms.

Link to original

A table is defined by its shape and material. So in the space of shapes and materials, there’s a region we’d classify as a table. This latent space is outside of our perception, but specific instantiations are made real by our thoughts and actions.
A table that’s never built, never imagined, and not found in nature simply doesn’t actually exist.

---

michael levin’s take:
Abstract properties of mathematics / geometry are true no matter the laws of physics.
A cell only has to evolve a voltage gated ion channel and it gets a truth-table for free.
There is such a space not just for mathematics, but also for kinds of minds, and life is good at exploiting it. This is not a random space, where interesting / useful emergent properties just so pop up from time to time, but it’s structured, it is incredibly vast, and we should map it, otherwise we just end up with a grab-bag, a catalog of things that hold. We need to assume there is a causal structure to it.
He doesn’t make the claim that this space is static ¹, but that it is at least partially unaffected by the physical world. We categorize the things that are constrained by these facts as “physics”, the ones
that exploit them as biology.

In his own words:

A Very Simple Argument – Michael Levin

(Transcript of: platonic space-1761908148632.webp)

1. There are specific facts of mathematics - “patterns” or forms. Examples: value of $e$, Feigenbaum’s constant, facts of number theory and topology, symmetry of $SU(2)$, amplituhedron, etc.

2. These patterns are surprising and forced on you once you choose basic assumptions (very few - just logic, apparently). You “get more out than you put in”. Start with set theory and get the specific value of $e$.

3. For some such pattern $P$:

   • There are aspects of physics and biology that are explained by recourse to the specifics of $P$. If you ask “why” long enough, you end up in the mathematics department.
   • In contrast, there is no aspect of the physical world (physical events/laws), and no amount of history (biological selection), that explain/set the properties of $P$.
   • If $P$‘s facts were different, biology and physics would be different.
   • It doesn’t work in the reverse: there is nothing you can change in the physical world to make $P$ be different.
     • Therefore, causality flows from these forms to the physical world (not in the temporal sense).
     • Therefore, these facts play important instructive roles. They cannot be ignored if you want to understand and tame evolution, bioengineering, etc.

4. Therefore:

   • physicalism is a non-viable theory: there are facts that are simply not “in” the physical world in any useful sense of “physics”.
   • Pythagoras knew this already. Let’s call the set of possible properties of $P$‘s “the Platonic Space”.

5. Optional hypotheses (optimistic metaphysical claim):

   • $P$ is drawn from a distribution that’s not a random collection but a structured space
   • Therefore, we have a research program: map the space, understand relationship between interface and which $P$ it channels.

6. Skeptical position: we cannot assume that low-agency models of math encompass all the residents of this Space. Some may be better described by behavioral science tools.

   • Therefore, some of the patterns that ingress into physics and biology may be “kinds of minds”.
   • Therefore, Dualism is viable. We already knew it was true in physics and biology; this suggests it’s also relevant in cognitive science.

7. Skeptical position: we cannot assume that biological materials, evolutionary search, etc. have any monopoly on hosting those patterns.

   • Therefore, perhaps algorithms/robots should be searched for surprising ingressions that are not just complexity or unpredictability, but well-understood cognitive competencies.
     

An attempt to rephrase levin’s argument from a materialist perspective:

There is one material world. Because of how matter organizes, there exist objective constraint-structures (attractors, symmetries, conservation laws, control geometries). Humans produce mathematical–conceptual spaces that model those constraints. Minds, embryos, and algorithms realize and exploit them (and we should too). Explanations run upward (composition) and downward (constraint), but all causation is materially implemented.

This should keep all the actionable implications for research, while removing the dualism?

From Experience to Math by Chris Fields:

Footnotes

1. And generally he’s calling it “platonic space” to connect to the notion of discovering the structured space of mathematics, but for kinds of minds; but says he’ll have to change the word “Platonic” eventually because his ideas don’t actually fully align with platonism. ↩