polynomial

Polynomial function

A real polynomial (function) is an expression of the form

$$f(x)=a_0+a_{1}x+a_2{x}^2+\dots +a_n{x}^n=\sum _{i=0}^n{a}_i{x}^i$$

where $a_0,a_1,\dots ,a_n$ are constants called the coefficients of the polynomial, and $n$ is a non-negative integer called the degree of the polynomial.
The domain is $\mathbb{R}$.

Root

A root (or zero) of the polynomial $f(x)$ is a value $r$ such that $f(r)=0$.

Root of multiplicity k

$r$ is a root of multiplicity $k$ of the polynomial $f(x)$ if

$$f(x)=\sum _{k=0}^n{a}_k{x}^n=(x-r{)}^k\cdot g(x)$$

for some polynomial $g(x)$ of order $n-k\ge 0$, with $g(r)\ne 0$.
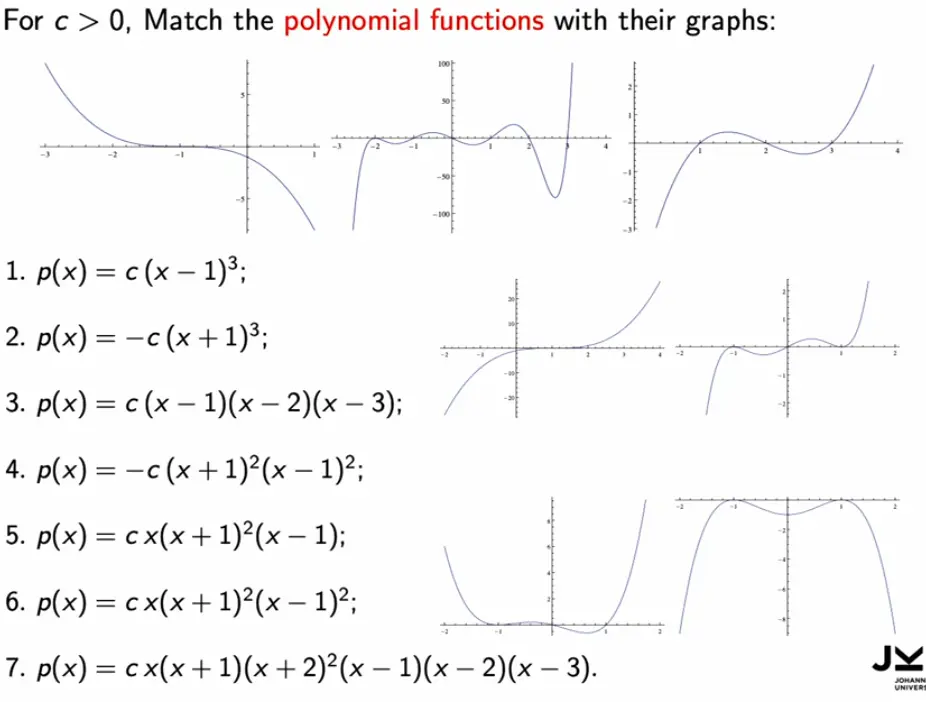
If $k$ is odd, the graph of $f(x)$ intersects the x-axis at $x=r$.
If $k$ is even, the graph of $f(x)$ touches the x-axis at $x=r$ without intersecting it.

$f(x)=x^2(x-1)(x+1)$

The polynomial $f(x)=x^2(x-1)(x+1)$ has roots at $x=-1,0,1$.
The root at $x=0$ has multiplicity 2 (even), so the graph touches the x-axis at this point.
The roots at $x=-1$ and $x=1$ have multiplicity 1 (odd), so the graph intersects the x-axis at these points.
Since the leading coefficient (of $x^4$) is even, the graph looks like a $\cup$ at the ends.
In total, the function looks like a “W” shape.

Note

We expect a polynomial of degree $n$ to have up to $n-1$ inflection points.
Odd powers always have at least one real root .

EXAMPLE

We can add/sub polynomials by add/sub their coefficients.

This makes them easy to work with for computers.
They’re also easy to differentiate/integrate symbolically.

fundamental theorem of algebra

Fundamental Theorem of Algebra

Let $a_k\in \mathbb{C}$ for $k=0,1,2,\dots n$, such that $a_n\ne 0$. Then the polynomial $P:\mathbb{C}\to \mathbb{C}$ defined by

$$\sum _{k=0}^n{a}_k{z}^k=a_n\prod _{k=1}^n(z-z_k)$$

has exactly $n$ roots $z_1,z_2,\dots ,z_n\in \mathbb{C}$, counted with multiplicity (i.e., some roots may be repeated).
In other words, every non-constant polynomial with complex coefficients has at least one complex root.

Link to original