complex number

Steve Brunton Playlist

---

Complex numbers are necessary in order to solve all polynomials (e.g. $x^2+1=0$).
The solutions to polynomials (including complex polynomials) are closed under the complex numbers (i.e. any polynomial has solutions $\in \mathbb{C}$).

Imaginary unit: $i=\sqrt{-1}$
A complex number has a real and an imaginary part, in the cartesian form:
$z=x+iy=\text{Re}(z)+i\cdot \text{Im}(z)\text{Re}(z),\text{Im}(z)\in \mathbb{R}$

Arithmetic with complex numbers in cartesian form.

Let: $z_1=x_1+i{y}_1$ $z_2=x_2+i{y}_2$

$$\text{displaylines}\begin{array}{rl}\text{Add/Sub:}& z_1\pm z_1=(x_1\pm x_2)+i(y_1\pm y_2)\\ \text{Mul:}& z_1{z}_2=(x_1+i{y}_1)(x_2+i{y}_2)=x_1{x}_2-y_1{y}_2+i(y_1{x}_2+y_2{x}_1)\\ \text{Div:}& \frac{x_1+i{y}_1}{x_2+i{y}_2}\cdot \underset{\frac{{\bar{z}}_2}{{\bar{z}}_2}=1}{\underbrace{\frac{x_2-i{y}_2}{x_2-i{y}_2}}}=\frac{z_1{\bar{z}}_2}{x_2^2+y_2^2}=\frac{z_1{\bar{z}}_2}{|z_2{|}^2}\end{array}$$

The laws of commutative, associativity and the distributive property apply. The neutral element is $0$.

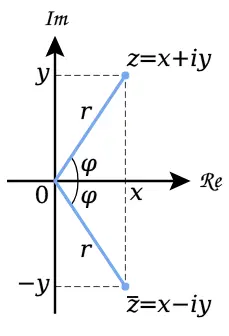
complex conjugate

Complex conjugate

The complex conjugate of a complex number $z=x+iy$ is $\bar{z}=x-iy$
The sign in front of $i$ (or the angle) is flipped, the magnitude stays the same:

$\overline{z_1+z_1}={\bar{z}}_1+{\bar{z}}_2$
$\overline{z_1\cdot z_1}={\bar{z}}_1\cdot {\bar{z}}_2$
$\frac{z+\bar{z}}{2}=x=\text{Re}(z)\in \mathbb{R}$
$\frac{z-\bar{z}}{2i}=y=\text{Im}(z)\in \mathbb{R}$
$z\cdot \bar{z}=x^2-iyx+iyx-(iy{)}^2=x^2+y^2=|z{|}^2$

Solutions to polynomials with real coefficients come in conjugate pairs: If $a+bi$ is a root, so is $a-bi$.

Link to original

The magnitude of a complex number $z=x+iy$ is its absolute value/radius $|z|=\sqrt{x^2+y^2}=\sqrt{z\bar{z}}=R$

$i^n$

$i$ to the power of $n$ cycles every four steps:

$$i^n=\{\begin{array}{ll}1& n\mathrm{mod}4=0\\ i& n\mathrm{mod}4=1\\ -1& n\mathrm{mod}4=2\\ -i& n\mathrm{mod}4=3\end{array}$$

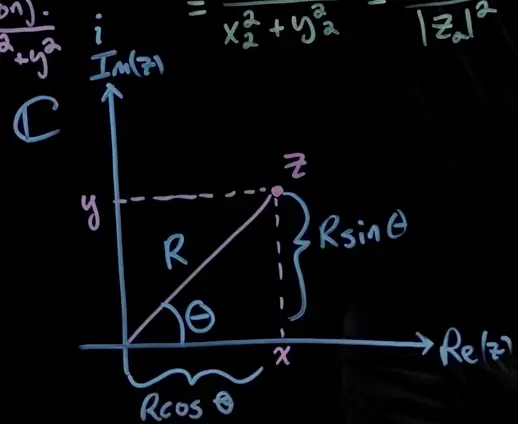
Polar coordinates / planar form:

Instead of the real part being $x$ coordinate and imaginary part being the $y$ coordinate, we represent the number in terms of a radius $R$ and an angle $\theta$:
$z=[R;\theta ]$
$\theta =\arctan \left(\frac{z}{b}\right)$
$x=R\cdot \cos (\theta )$
$y=R\cdot \sin (\theta )$

With the help of euler’s formula:

Transclude of euler’s-formula#^d23d73

we can write it as:

$$z=R[\cos (\theta )+i\sin (\theta )]=R{e}^{i\theta }$$

Btw:
$1+i=[\sqrt{2};\frac{\pi }{4}]$
$1-i=[\sqrt{2};-\frac{\pi }{4}]$
This looks weird–until you look at the graphed polar form!

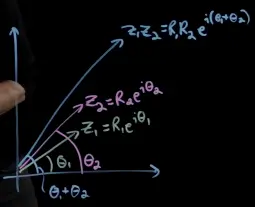
Arithmetic with complex numbers in polar form.

Complex multiplication becomes easy–we multiply the radii (absolute values) and add the angles (arguments):

$$R_1{e}^{i{\theta }_1}{R}_2{e}^{i{\theta }_2}=R_1{R}_2{e}^{i({\theta }_1+{\theta }_2)}$$

In the resulting complex vector, the resulting radius is a multiple of the real parts (like in usual multiplication) but the angles simply add:

Similarily for division:

$$\frac{z_1}{z_2}=\frac{R_1}{R_2}{e}^{i({\theta }_1-{\theta }_0)}$$

Potentiation is just multiplying the radius $n$ times and adding the angle $n$ times:

$$z^n=R^n{e}^{in\theta }=R^n[\cos (n\theta )+i\sin (n\theta )]$$

Powers of complex numbers $|z|>1$, $|z|<1$

EXAMPLE

Let: $w^2=zz\in \mathbb{C}$
We are looking for a $z=[R;\theta ]$.
Solution: $w_1=[\sqrt{R};\frac{\theta }{2}]$, $w_2=[\sqrt{R},\frac{\theta }{2}+\pi ]$ (plus $\pi$ because if we square, we add $2\pi$ coming full circle on the same point).

---

Let: $w^n=z$
Solution: $w_1=[\sqrt[n]{r};\frac{\theta }{n}]$, $w_2=[\sqrt[n]{r};\frac{\theta }{n}+\frac{2\pi }{n}]$, $w_3=[\sqrt[n]{r};\frac{\theta }{n}+\frac{4\pi }{n}]$, …, $w_n=[\sqrt[n]{r};\frac{\theta }{n}+\frac{2\pi (n-1)}{n}]$
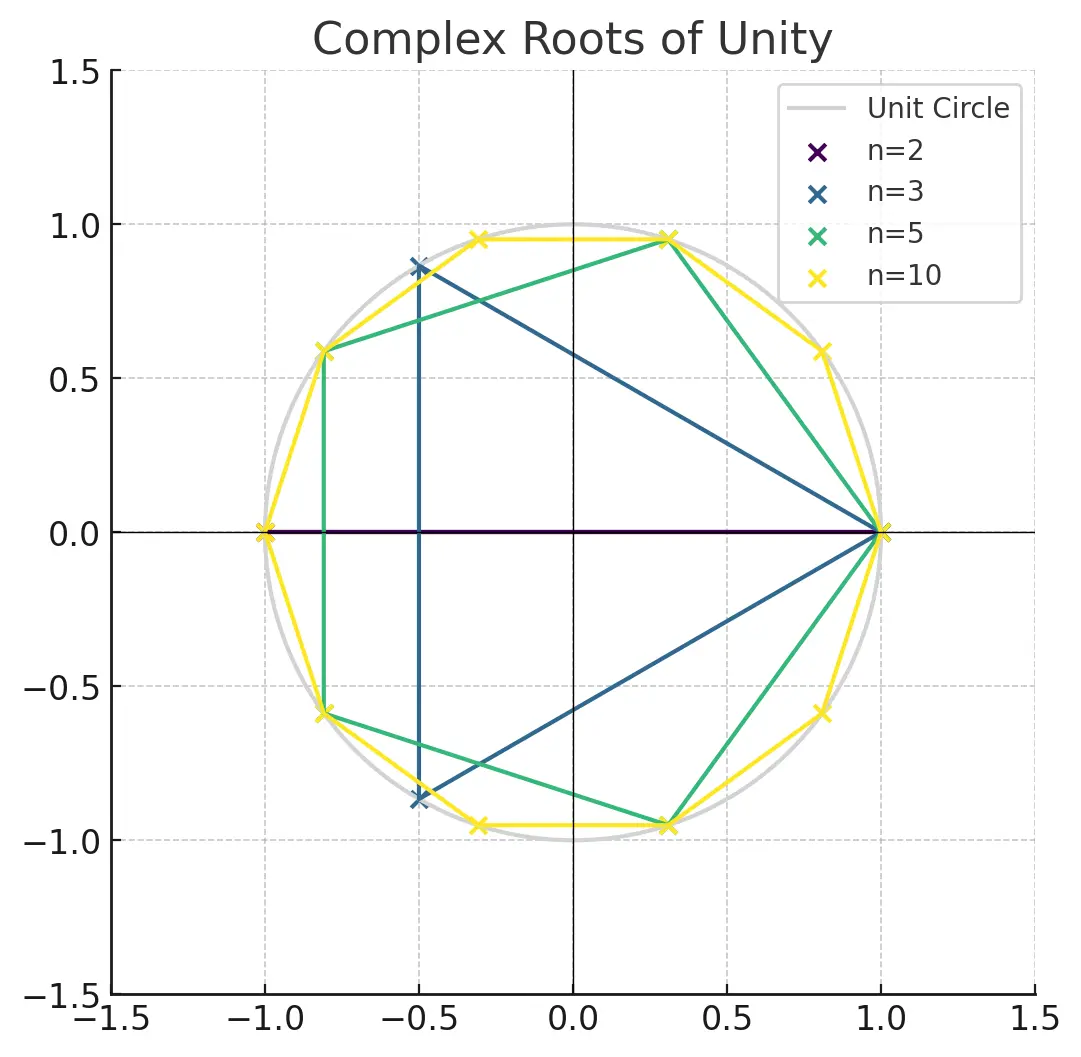
If $z=1$, these solutions are called the n-th complex roots of unity:

roots of unity

A root of unity is any complex number that, when raised to a positive integer power $n$, equals $1$.

$z\in \mathbb{C}$ is an $n^{\text{th}}$ root of unity if:

$$\begin{array}{r}{z}^n=1\end{array}$$

These roots are evenly spaced on the unit circle in the complex plane and can be represented as:

$$\begin{array}{r}{\zeta }_n^k=e^{2k\pi i/n}=\cos \left(\frac{2\pi }{n}\right)+i\sin \left(\frac{2\pi }{n}\right)\end{array}$$

for $k=0,1,\dots n-1$. The angles between the consecutive roots are all equal, and their magnitudes are all equal to $1$–they lie on the unit circle, hence roots of unity.

3b1b: generating functions shows an application of roots of unity.

For any root of unity ${\zeta }_n^k$, multiplying it by itself $n$ times gives us 1.

E.g. for the 5th roots of unity ${\zeta }_k=e^{2\pi ik/5}$ and their powers: ${\zeta }_1=e^{2\pi i/5}$ (rotation by 72°):

$${\zeta }_1\to {\zeta }_1^2\to {\zeta }_1^3\to {\zeta }_1^4\to {\zeta }_1^5=1$$

${\zeta }_2=e^{4\pi i/5}$ (rotation by 144°):

$${\zeta }_2\to {\zeta }_2^2\to {\zeta }_2^3\to {\zeta }_2^4\to {\zeta }_2^5=1$$

${\zeta }_3=e^{6\pi i/5}$ (rotation by 216°):

$${\zeta }_3\to {\zeta }_3^2\to {\zeta }_3^3\to {\zeta }_3^4\to {\zeta }_3^5=1$$

${\zeta }_4=e^{8\pi i/5}$ (rotation by 288°):

$${\zeta }_4\to {\zeta }_4^2\to {\zeta }_4^3\to {\zeta }_4^4\to {\zeta }_4^5=1$$

${\zeta }_5=e^{10\pi i/5}=1$ (rotation by 360°):

$$1\to 1\to 1\to 1\to 1$$

Each root, when multiplied by itself repeatedly, traces out its own unique path through the fifth roots before arriving at 1 after exactly five multiplications.

Link to original

EXAMPLE

Let: $z^2+pz+q=0$
$z^2+pz+q=\underset{(z+\frac{p}{2}{)}^2}{\underbrace{z^2+pz+\frac{p^2}{4}}}+q-\frac{p^2}{4}$
$z+\frac{p}{2}=\pm \sqrt{\frac{p^2}{4}-q}$
$z_{1,2}=-\frac{p}{2}\pm \sqrt{\frac{p^2}{4}-q}$
$(z-z_1)(z-z_2)⟹\{\begin{array}{l}p=-z_1-z_2\\ q=z_1{z}_2\end{array}$ (wasn’t explained further)

There only are general formulas for solving any polynomial—where you just need to input the coefficients of the different degrees–up to degree four.

Todo

3b1b:
https://youtu.be/sD0NjbwqlYw (rieman zeta)

overview of complex functions

$f(z)=z^n=(R[\cos (\theta )+i\sin (\theta )]{)}^n$ … power function
$f(z)={\sum }_{k=0}^n{a}_k{z}^k$ … power series
$f(z)=\frac{{\sum }_{k=0}^n{a}_k{z}^k}{{\sum }_{j=0}^m{b}_j{z}^j}$ … rational function
$f(z)={\sum }_{k=0}^{\infty }{a}_k(z-z_0{)}^k$ … taylor series (centered around any point $z_0$)

The above functions are called analytic functions, they are continous and smooth everywhere, taking derivatives makes sense, you can do calculus, the finite sums are well-defined smooth functions.

taylor series convergence

→ only convergent if $L={\lim }_{k\to \infty }\mid \frac{a_{k+1}}{a_k}\mid \text{exists}$
→ then, $f$ converges for $\mid z-z_0\mid <\frac{1}{L}$ … the series converges within the radius $\frac{1}{L}$ from $z_0$, meaning it is a nice and smooth analytic function

trig funcs:
$\sin (z)=\frac{e^{iz}-e^{-iz}}{2i}$ # TODO homework with chatty to verify taylor series expansion…, that the terms cancel | vid3 @ 18:xx ff. some more stuff to practice