softmax

• Normalizes values between 0 and 1; Always bigger than zero → exp
• Creates a probability distribution: Values sum to 1.
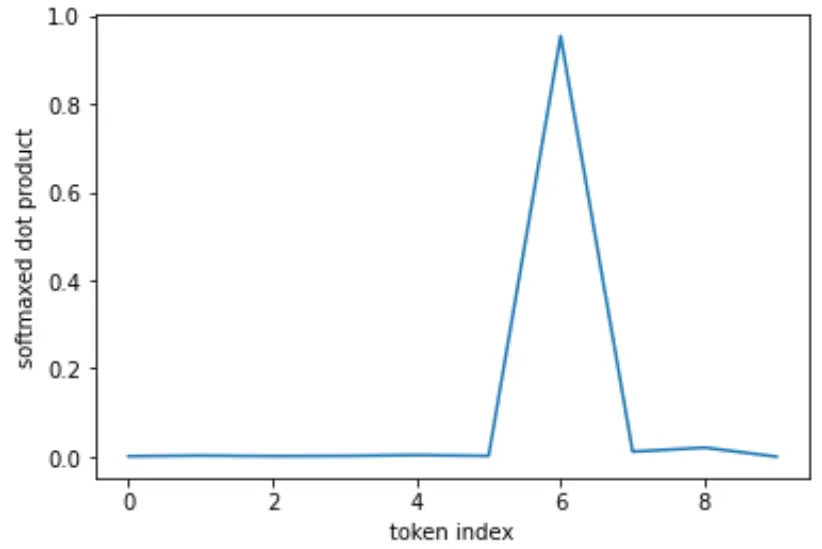
• Exaggerates biggest value. Other tend to 0 quickly.
• Distribution stays the same if a constant is added to the input: $\sigma (\vec{x}+\vec{c})=\sigma (\vec{x})$
• Soft, since in contrast to $\max$, it preserves simmilar values and doesn’t only take the highest (one-hot) (but it has similar behavior, see below).
• Differentiable, as opposed to $\max$.
• Roughly constant gradient.
• Commonly used for Classification or Attention.

$$\sigma (\vec{z}{)}_i=\frac{e^{z_i/\tau }}{{\sum }_K^{j=1}{e}^{z_j/\tau }}$$

$\tau \dots$ temperature

Temperature is just the inverse of multyplying the input by a constant.

If the constant is large (temperature is small), then the input gets sharpened towards the max.
If the constant is small (temperature is high), then the distribution is more diffused / uniform.
See this visualization notebook of how scaling the inputs affects the distribution.

Softmax has noise-supression properties – like [max] – the highest value dominates, others are driven to $0$.

This can be a useful feature for singling-out tokens in softmax scaled dot product attention.
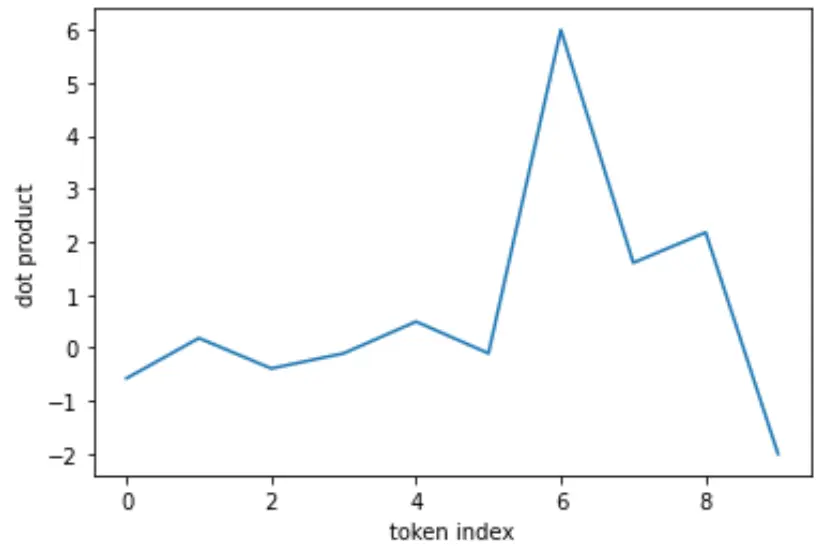
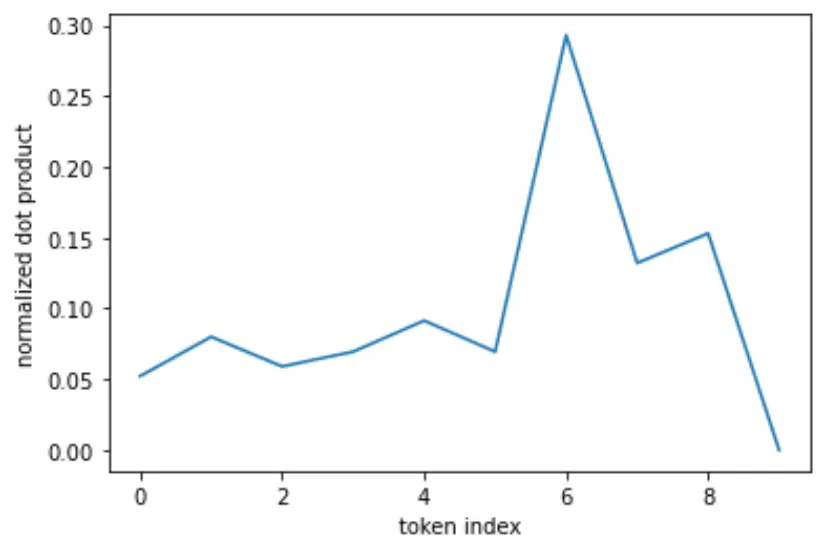
Raw values:

Normalized:

Softmax:

import torch
t = torch.tensor([-1, 1, 0, 0.5, 0.25, -0.5])
t.softmax(dim=-1)
# tensor([0.0482, 0.3565, 0.1311, 0.2162, 0.1684, 0.0795])
(2*t).softmax(dim=-1)
# tensor([0.0102, 0.5573, 0.0754, 0.2050, 0.1243, 0.0277])
(t+10).softmax(dim=-1)
# tensor([0.0482, 0.3565, 0.1311, 0.2162, 0.1684, 0.0795])

Visualization Notebook
Understanding softmax and the negative log-likelihood