scaled dot product attention

Scaled dot product attention is at the heart of the self-attention and cross-attention mechanisms (refer to these notes for a full explanation).

Scaled dot product attention

The cosine similarity scores are scaled down by $\sqrt{d_k}$ in order to keep the variance at $1$:

$$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V$$

Why do we want a variance of 1?

For softmax, we want the inputs to be fairly diffuse, otherwise it will converge towards one-hot vectors / argmax:

Temperature is just the inverse of multyplying the input by a constant.

If the constant is large (temperature is small), then the input gets sharpened towards the max.
If the constant is small (temperature is high), then the distribution is more diffused / uniform.
See this visualization notebook of how scaling the inputs affects the distribution.

Link to original

Otherwise, each token would only attend to a single other token, which is not what we want, especially not at initialization

Why is $\text{Var}(Q{K}^T)=d_k$ ?

If we assume that $\mathbf{q}$ and $\mathbf{k}$ are $d_k$-dimensional vectors whose components are independent random variables with mean $0$ and variance $1$, then their dot product has mean $0$ and variance $d_k$.

Explanation:
$q_i$ and $k_i$ being independent random variables with mean zero and variance one gives us the following properties:
$\mathbb{E}[q_i]=\mathbb{E}[k_i]=0$
$\text{Var}(q_i)=\mathbb{E}[q_i^2]-\cancel{\mathbb{E}[q_i{]}^2}=1$
$\text{Var}(k_i)=\mathbb{E}[k_i^2]-\cancel{\mathbb{E}[k_i{]}^2}=1$
→ $\text{Var}(\mathbf{q}\cdot \mathbf{k})=\mathbb{E}[(\mathbf{q}\cdot \mathbf{k}{)}^2]$
We are left with calculating the second moment of the joint distribution.
We split the calculation such that the diagonal entries are calculated seperately from the off-diagonal entries.

$$\begin{array}{rl}\mathbb{E}[(\mathbf{q}\cdot \mathbf{k}{)}^2]& =\mathbb{E}[\sum _{i=1}^{d_k}{q}_i{k}_i\sum _{j=1}^{d_k}{q}_j{k}_j]\\ & =\mathbb{E}\left[{\left(\sum _{i=1}^{d_k}{q}_i{k}_i\right)}^2\right]\\ & =\mathbb{E}\left[\sum _{i=1}^{d_k}\sum _{j=1}^{d_k}{q}_i{k}_i{q}_j{k}_j\right]\\ & =\mathbb{E}\left[\sum _{i=1}^{d_k}{q}_i^2{k}_i^2+\sum _{i\ne j}{q}_i{k}_i{q}_j{k}_j\right]\\ & =\sum _{i=1}^{d_k}\text{cancelto}1\mathbb{E}[q_i^2]\text{cancelto}1\mathbb{E}[k_i^2]+\sum _{i\ne j}\cancel{\mathbb{E}[q_i]}\cancel{\mathbb{E}[k_i]}\cancel{\mathbb{E}[q_j]}\cancel{\mathbb{E}[k_j]}\\ & =d_k\end{array}$$

Why softmax?

It’s differentiable.
It converts arbitrary scores (logits) into a probabilities.
It has a non-linear “winner-take-all” characteristic: It amplifies strong signals (high correlation scores) and suppresses noise (low correlation scores), which seems useful for focusing attention on the most relevant tokens:

Softmax has noise-supression properties – like [max] – the highest value dominates, others are driven to $0$.

This can be a useful feature for singling-out tokens in softmax scaled dot product attention.
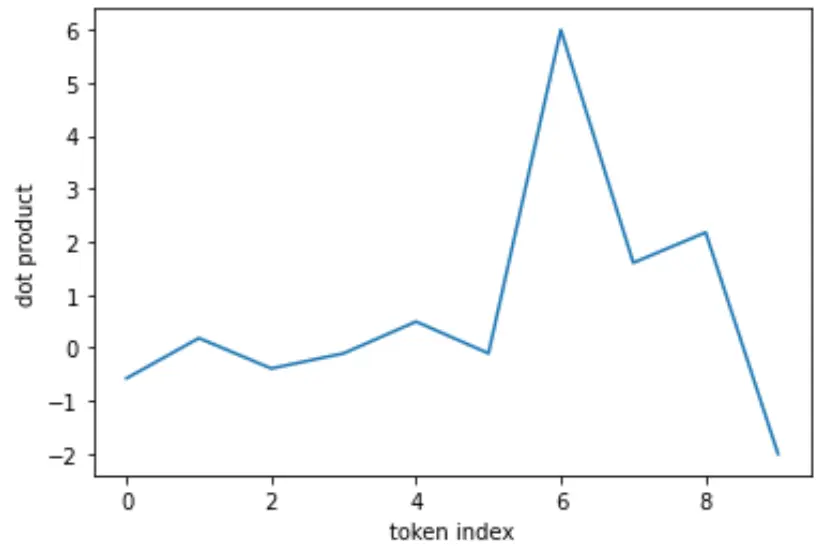
Raw values:

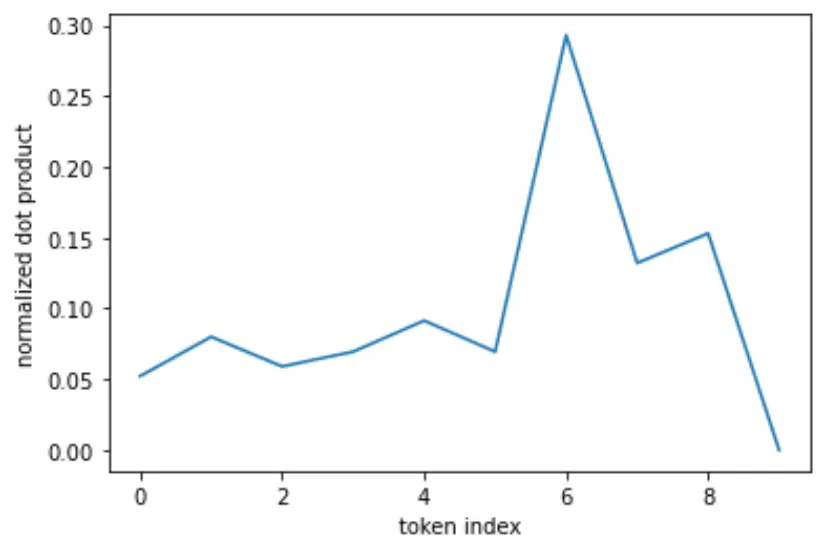
Normalized:

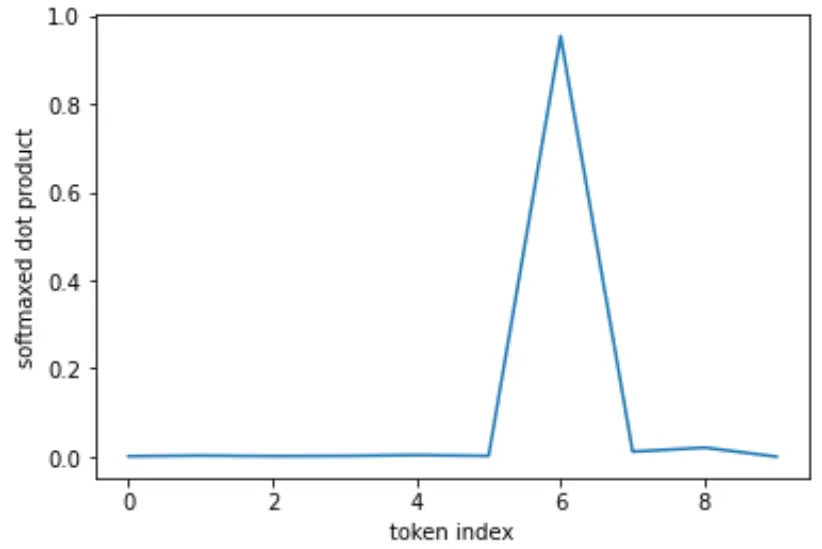
Softmax:

Link to original

One issue with softmax is that for growing sequence lengths, the attention on individual tokens gets diffused, making it easier for signal to get lost in noise.

The distribution becomes progressively more flat, entropy increases, and the largest value becomes much smaller.
With growing sequence length so does the requirement to produce outlier-ly large values to overwhelm all the others and achieve sharpness. We end up with many small spikes rather than few large ones.

attention sinks might be a result of this, reducing the weights placed on other, informative tokens, just to redue magnitude of the output.

This and other issues prompt the search for alternatives to softmax for attention, or how to fix its bugs (Softmax attention is a fluke):

Softmax's Behavior with Variable Sequence Lengths

Entropy/Sharpness Drift: As the sequence length ($N$) increases, a standard softmax distribution tends to become flatter (higher entropy, smaller maximum value) for the same range of input logits. To maintain “sharp” attention (concentrated on a few tokens) in longer sequences, the model needs to produce disproportionately large logit values for the target tokens to overcome the larger denominator sum.
Difficulty Achieving “Null Attention”: Softmax forces the weights to sum to 1. A token cannot easily choose to “attend to nothing” or significantly reduce the overall magnitude of the attention layer’s contribution, as the denominator $\sum e^{z_j}$ is directly tied to the numerators $e^{z_i}$. Even if all correlations are low or negative, softmax will still produce a distribution summing to 1.
Emergence of “Attention Sinks”: As a maladaptive workaround for the lack of true null attention, models often learn to dump large amounts of attention weight onto semantically meaningless tokens (like BOS, padding tokens, or even punctuation). By attending heavily to a “dummy” token (whose value projection might also be learned towards zero), a token can effectively reduce the influence of other informative tokens while still satisfying the sum-to-1 constraint.
Training Instability Hypothesis in Causal LMs: During training of causal models (like GPT), different tokens effectively attend to sequences of different lengths (from 1 up to the context window size) simultaneously. However, they all share the same Q/K projection matrices. The optimal Q/K vector norms (to achieve desired attention sharpness) might differ depending on the effective sequence length. Short sequences might prefer lower norms (for softer attention), while long sequences might need higher norms (to fight entropy increase). These conflicting requirements on shared weights could lead to optimization challenges and instability.

Do We Need Softmax's Properties for Attention?

Why must weights be probabilities? Attention is about weighted mixing of information (value vectors). Does this mixing strategy have to be framed as a probability distribution? Other kernels (e.g., polynomials like $x^3$) can also provide noise suppression without the probabilistic interpretation.
Why must weights be positive? Could negative correlations be just as informative as positive ones? Perhaps the goal should be suppressing small (near-zero) correlations, rather than strictly enforcing positivity.
Why must weights sum to one? Does attention always need to output a convex combination of value vectors? Maybe allowing the layer to scale its output magnitude (e.g., weights summing to < 1 or > 1) could be beneficial, allowing the layer to control its influence.

Potential Fixes: Towards "Calibrated Attention"

The article proposes modifications to the attention mechanism to address these issues:

1. Sequence-Length Dependent Scaling: Instead of a fixed scaling factor (like $1/\sqrt{d_k}$), make the scaling dependent on the current sequence length $N$. This could potentially stabilize the entropy/sharpness of the attention distribution across different lengths. This could be a fixed formula or a learned function of $N$.
2. Denominator Bias: Introduce an additive bias term $B$ (could be fixed, e.g., +1 as in “Softmax-plus-one”, or learned, potentially also dependent on $N$) into the softmax denominator:

$${\text{attn\_weights}}_i=\frac{e^{z_i}}{{\sum }_j{e}^{z_j}+B}$$

This decouples the numerator and denominator slightly. If all $e^{z_i}$ are small relative to $B$, the weights can become very small, approaching zero, allowing for true “null attention” or partial attention (weights summing to < 1). This removes the need for attention sinks.