Hopfield Network

Hopfield networks are energy-based associative weight netowrks.

The goal of Hopfield nets (without hidden units) is to store patterns (learn a pattern and then access with only a part of the data; content-addressable memory “ associative memory”) by finding the configuration that leads to the lowest energy state.

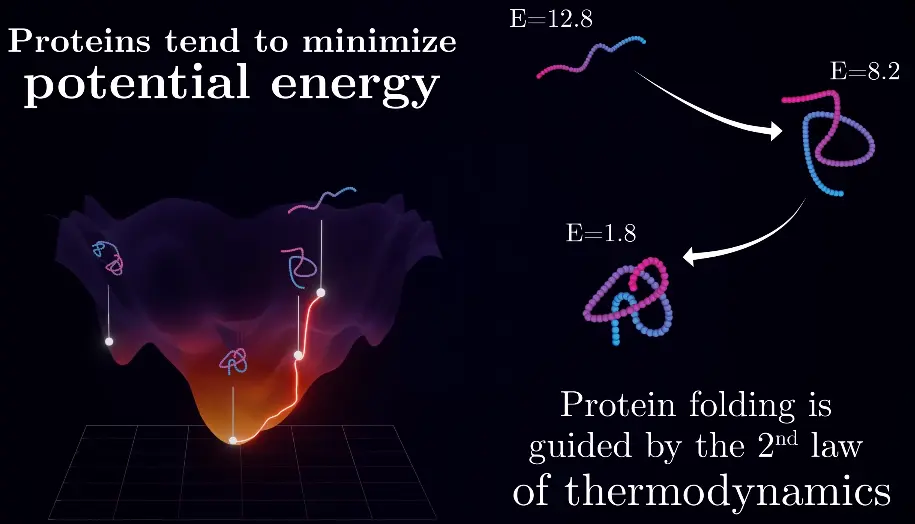
Protein folding is a similar problem to the one of Hopfield nets: Finding the lowest potential energy state of a protein:

It can fold quickly, since it doesn’t need to perform any search in the configuration space, but just needs to settle in the lowest energy state, following the energy gradients / path of least action, just like a ball that is thrown doesn’t move in squiggly lines.
The energy landscape is determined by the interaction rules of the atoms in the protein.

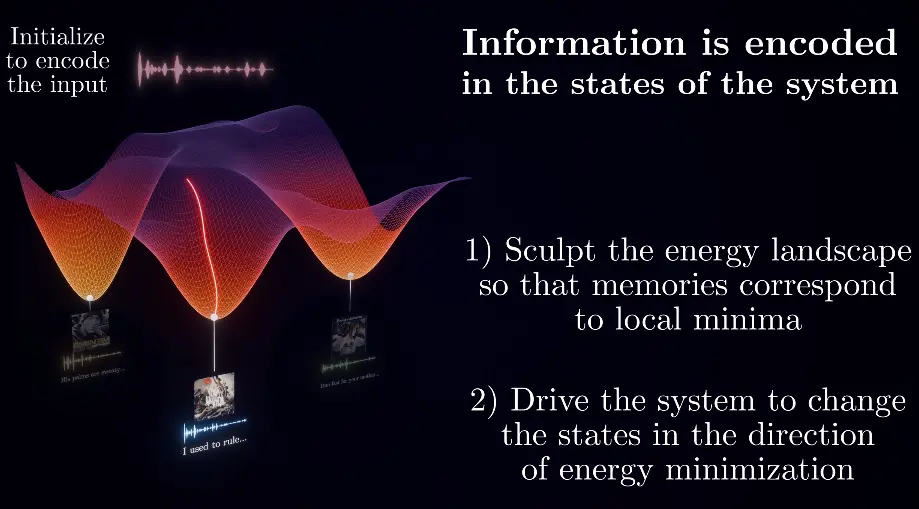
We can utilize this principle to store different information / concepts at different local minima of the energy landscape. By initializing the system with something close to the desired information, it “searches”, or rather automatically settles in the most similar state, which is the desired information (after the network has been trained to store this information for this particular state).

TLDR

You encode a (binary) value in each of the neurons, let the connection’s weights between them be changed to reach an energy minimum for this pattern. This way you can also encode multiple patterns. If units are in a random state and you set some of them to be a part of the sequence you want to retrieve, it settles in the desired state and you get the entire sequence back. You can even remove a few units theoretically, and the rest will still work fine.

Energy function and learning

Binary Hopfield nets are made up of units / nodes / neurons which are an abstract representation of biological neurons, a state of +1 corresponding to a firing neuron and -1 to a silent neuron (they can also be 0 and 1).
The network is fully connected, i.e. each neuron is connected to every other neuron.
Weights $w_{ij}\in \mathbb{R}$
Neuron states / “activities” $x_i\in \{-1,+1\}$
The system if further simplified by the use of symmetric connection, which means, that two neurons share a single weight. The connection weight from neuron $i$ to $j$ is the same as the other way round ($w_{ij}=w_{ji}$).

$w_{ij}>0$ … promotes alignment of the states of the two neurons ($x_i=x_j$).
$w_{ij}<0$ … promotes anti-alignment of the states of the two neurons ($x_i=-x_j$).
The product of two connected nodes is positive if they have the same sign and negative if they have opposite signs.

$$\begin{array}{rl}{\text{Edge Happiness}}_{ij}& =w_{ij}{x}_i{x}_j\\ \text{Network Happiness}& =\sum _{(i,j)\in E}{w}_{ij}{x}_i{x}_j\\ \text{Optimization Goal:}& \underset{x}{\max }\sum _{(i,j)\in G}{w}_{ij}{x}_i{x}_j\\ & \text{or equivalently}\\ & \underset{x}{\min }-\sum _{(i,j)\in G}{w}_{ij}{x}_i{x}_j\end{array}$$

In other words: We want to minimize the degree of tension, i.e. the unalignedness of the nodes in the network. This conflict is what we call energy ($E=-{\sum }_{(i,j)\in E}{w}_{ij}{x}_i{x}_j$).

There is still a distinction between learning and inference in Hopfield networks:

• Learning: Adjusting the weights to store patterns - shaping the energy landscape.
• Inference: Traversing the energy landscape step by step by changing the states of the neurons.

Inference - Binary Threshold Decision Rule

For inferring a pattern or in general a minimum, we start with the closest state we have to that pattern, or a random state. We then iteratively go through each neuron and apply the following rule in order to determine whether it should change its state:
The neighbouring neurons “vote” whether the neuron should change its state:

$$\begin{array}{rl}{h}_i& =\sum _{j\ne i}{w}_{ij}{x}_j{x}_j\\ x_i& =\{\begin{array}{ll}+1& \text{if }{h}_i\ge 0\\ -1& \text{if }{h}_i<0\end{array}\end{array}$$

A positive $h_i$ means that the neuron should be on, a negative value means it should be off. The neuron then changes its state accordingly.
This way, the neurons more and more agree with each other until we reach a point where flipping any neuron would increase the energy of the network. A minimum / “steady state” is reached / converged to a stable configuration.

EXAMPLE

$x_{?}=-4\cdot 1+0\cdot 3+0\cdot 3\le 0\to 0$
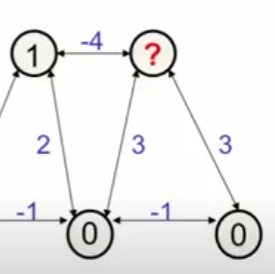
If we look at the unit in the bottom middle, we see that it wants to turn on … we let it:

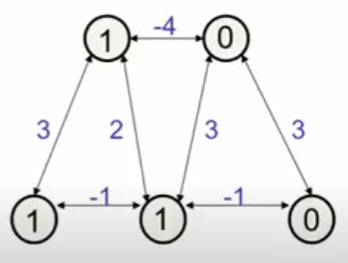
Now, none of the remaining units want to be changed → local energy minimum (=-4).
Local minimum, since this is not the lowest possible energy.
b.whatsapp.com/
[!note] Convergence is only guaranteed for symmetric connections - where updating by flipping one by one based on this local update rule is equivalent to global energy based descend.

Learning

In the simplest case, we have one pattern $\vec{\xi }=[x_1,x_2,\dots ,x_N{]}^T$ we want to store.
To find the energy of the pattern we want to store:

$$E(\text{pattern})=-\sum _{(i,j)\in G}{w}_{ij}{\xi }_i{\xi }_j$$

Energy is lowest when all weights maximally align with pariwise states in the memory patterns, i.e. we need to set each weight as: $w_{ij}\leftarrow {\xi }_i{\xi }_j$, strengthening connections between neurons that have matching pairwise relationships (that’s hebbian learning).
Multiple patterns can be stored as by simply adding the weights for each pattern.

$$\text{displaylines}{w}_{ij}=\underset{w_{ij}^1}{\underbrace{{\xi }_i^1{\xi }_j^1}}+\underset{w_{ij}^2}{\underbrace{{\xi }_i^2{\xi }_j^2}}+\dots +\underset{w_{ij}^m}{\underbrace{{\xi }_i^m{\xi }_j^m}}$$

The resulting energy landscape will also look like the individual landscapes added.

Including a bias term, the global quadratic energy function looks like this:

$$\text{displaylines}E=-\underset{\text{bias term}}{\underbrace{\sum _i{x}_i{b}_i}}-\underset{\text{quadratic term (2 units)}}{\underbrace{\sum _{i<j}{x}_i{x}_j{w}_{ij}}}$$

This energy function makes it possible for each unit to compute locally how its state affects the gloabal energy:

$$\text{displaylines}\text{Energy gap}=\Delta E_i=E(x_i=0)-E(x_i=1)=b_i+\sum _j{x}_j{w}_{ij}$$

Energy gap = difference between energy when neuron $i$ is off / on.
To optmize it, you literally just apply the binary threshold decision rule sequentially to each neuron, till the network settles.

The hamiltonian of the Hopfield Network is identical to the ising model, except that the interaction strength is not constant, and very similar to attention!

For a hopfield network:

$$H=-\sum _{i\ne j}{W}_{ij}{s}_i{s}_j$$

$W=X_i^T{X}_j$ is the weight / interaction matrix, which encodes how patterns are stored, rather than being a simple interaction constant.
In a simplified form, the update rule of the HFN is:

$$\Delta s_i\approx \sum _j(X_i^T{X}_j)s_j$$

And for attention:

$$\Delta s_i\approx \sum _j\sigma (K_i^T{Q}_j)V_j$$

Tokens in self-attention are just like spins in the ising model, but instead of spins, they are vectors in higher dimensional space, with all to all communication, self-organizing to compute the final representation.

Link to original

Oscilations!

If units make simultaenous decisions, the energy could go up. With simultaneous parallel updating, we can get oscilations (with a period of 2).
If the updates occur in parallel but with random timing, the oscillations are usually destroyed.

As seen above, if we use activities of 1 and -1, we can store a state vector by incrementing the weight between any two units by the product of their activities:

$$\Delta w_{ij}=x_i{x}_j$$

Biases are treated as weights from a permanently on unit.
With states of 0 and 1, the rule is only slightly more complicated:

$$\Delta w_{ij}=4\left(x_i-\frac{1}{2}\right)\left(x_j-\frac{1}{2}\right)$$

The weight update rule is a very simple rule that is not error-driven, which is both its strength and weakness.

• It’s strong because it is not error-driven: We are not comparing what we would have predicted with what the right answer is, and then making small adjustments.
  • Weight updates can be done online (and locally), as you just go through the data once, and you are done.
  • It’s weak, because it’s not a very efficient way of storing information.

Limitations: Storage capacity

You can only store $0.15N$ memories with $N$ units.
With $N$ bits per memory (weights, biases, state), total information stored $=0.15N^2$ bits.
What limits the storage capacitiy of Hopfield Nets is, that for each new pattern / configuration, you want to create a combination of the weights that creates a new energy minimum, like so:

but at some point, when the patterns will be too closeby they start to overlap:

So you will recall a blend of the original memories.

A strategy to prevent this is to let the network settle in a random state, apply the negative of the learning rule and thus pulling up deep spurious minima, i.e. removing them and reconstructing the original patterns (unlearning).
A simmilar proccess could be happening while we dream.

The total combinations of states in a binary HN is $2^N$, which can be thought of the corners of an $N$-dimensional (hyper)cube (which scale with the power of 2).

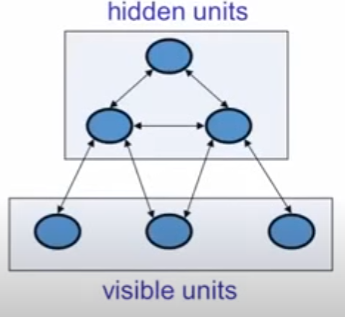
Hopfield Networks with hidden units

Instead of using the net to store memories, use it to construct interpretations of sensory input.

• The input is represented by the visible units.
• The interpretation is represented by the states of the hidden units.
• The badness of the interpretation is represented by the energy

Stochastic binary units

(See first: simulated annealing for intuition)

$$\text{displaylines}p(s_i=1)=\frac{1}{1+e^{-\Delta E_i/T}}$$

$T$ … temperature.

Raising the temperature is equivalent to decreasing energy gaps between configurations of the units.

$T\to \infty ⇝p\to \frac{1}{2}$, So at a high temperature (much noise), the state of unit $i$ is randomly on / off.

At $T\to 0$ (as in a regular Hopfield net), the sign of $\Delta E$ decides whether the state is on or off. Behaviour is deterministic: It will always adopt the lowest energy state, depending on whether the unit is off or on.

References

Jeoff Hinton Talk about Hopfield nets and Boltzman Machines
CSC321: Introduction to Neural Networks and machine Learning Lecture 16: Hopfield nets and simulated annealing
The Physics Of Associative Memory

energy-based models
biologically inspired