Simmulated annealing is a probabilistic technique (employing a degree of randomness) for minimizing the energy of a system according to some energy function.
basically:
- you have a system with an energy function that you want to minimize (e.g. least distance between points; greatest accuracy of calculation; …)
- you probabilistically explore different configurations of your system
- you perturb your current state by a little bit - exploring your neighbouring states until you arrive at a state that has no neighbouring states with lower energy than your current state
- you don’t visit every neighbouring state but choose it probabilistically based on the energy values of the neighbours
- like this, you would easily end up in local minima/optima
- hence we add randomness (“temperature”) to the choosing function / “acceptance probability function”
- the temperature is annealed over time, (in the beginning you can literally jump out of local minima, eventually only the lowest energy neighbour is chosen again)
- no need for gradient descent
At each step, the simulated annealing heuristic considers some neighboring state s* of the current state s, and probabilistically decides between moving the system to state s* or staying in-state s. These probabilities ultimately lead the system to move to states of lower energy. Typically this step is repeated until the system reaches a state that is good enough for the application, or until a given computation budget has been exhausted. 1
The temperature can be thought of as stochastic noise, which helps jump over the local minima.
Examples
Overcoming minima

Simulated annealing searching for a maximum. The objective here is to get to the highest point. In this example, it is not enough to use a simple hill climb algorithm, as there are many local maxima. By cooling the temperature slowly the global maximum is found. 1
Temperature as stochastic noise
Start with lots of noise and slowly reduce the noise, so the system ends up in a deep minimum. High temperature is like flatening the enrgy landscape:
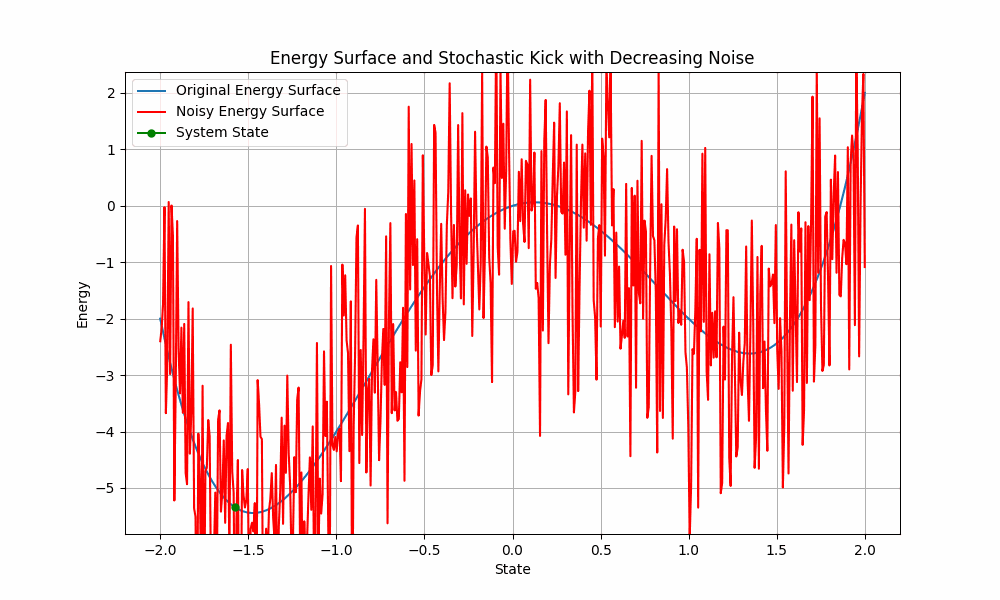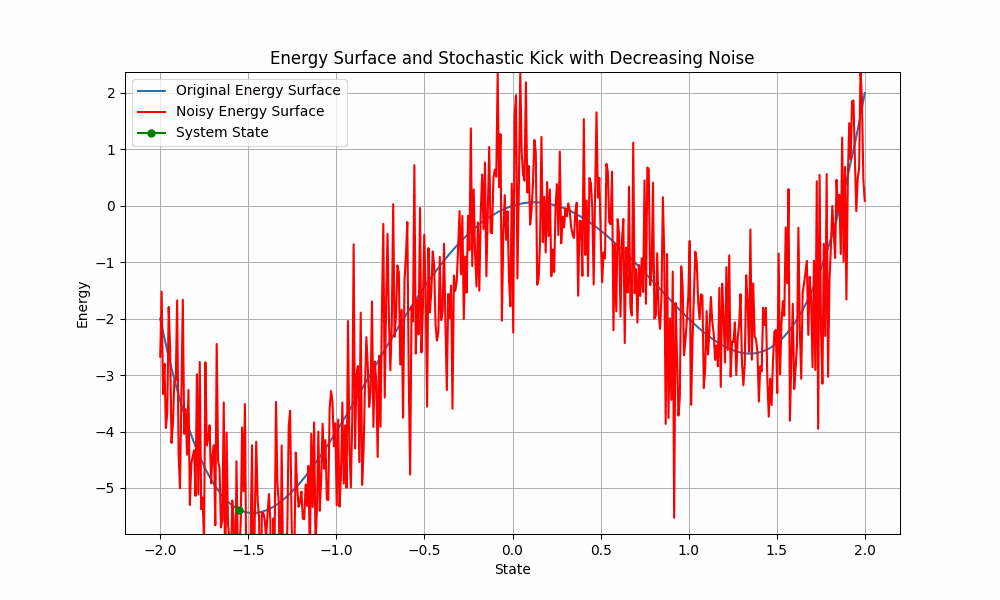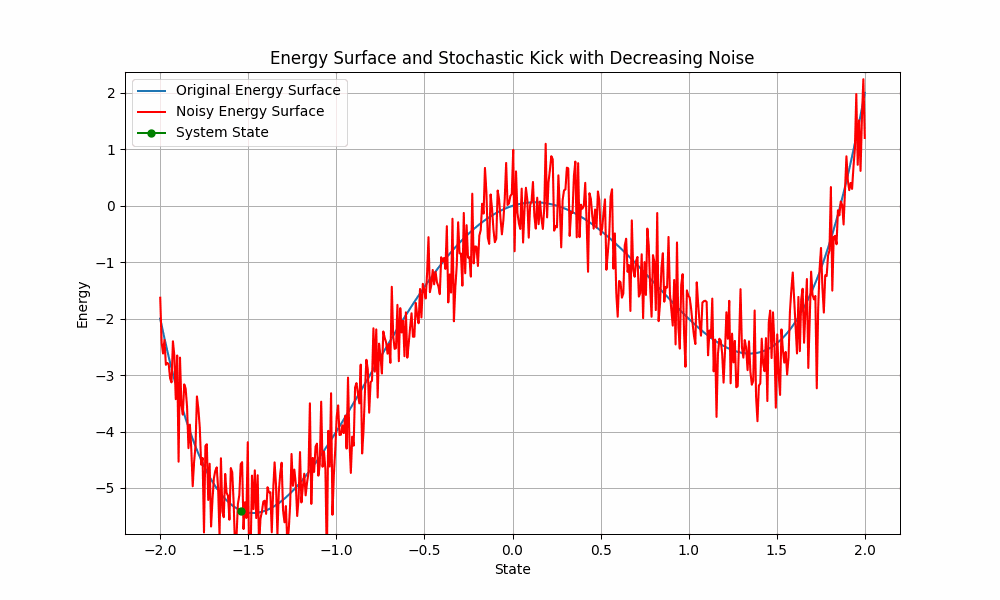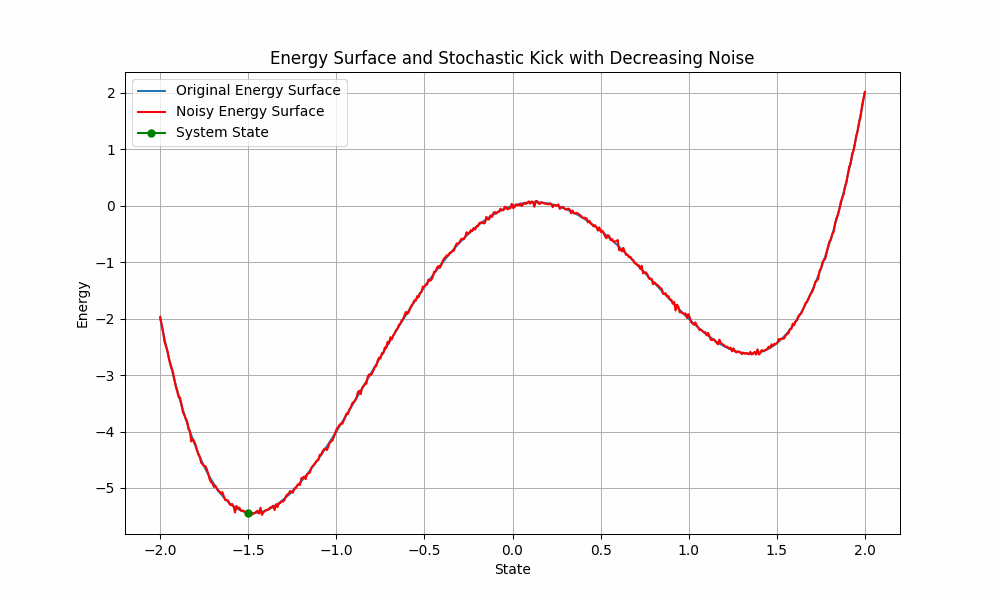
With high temperature, the probability to go to deeper states is higher, but not much higher than going from deeper to more shallow minima. So it is harder to stay at a deep minimum due to the noise, which flattens the landscape.
In the low temperature system, the probability to cross barriers / local minima is much lower, however the ratio of particles ending up in a good state is much better.
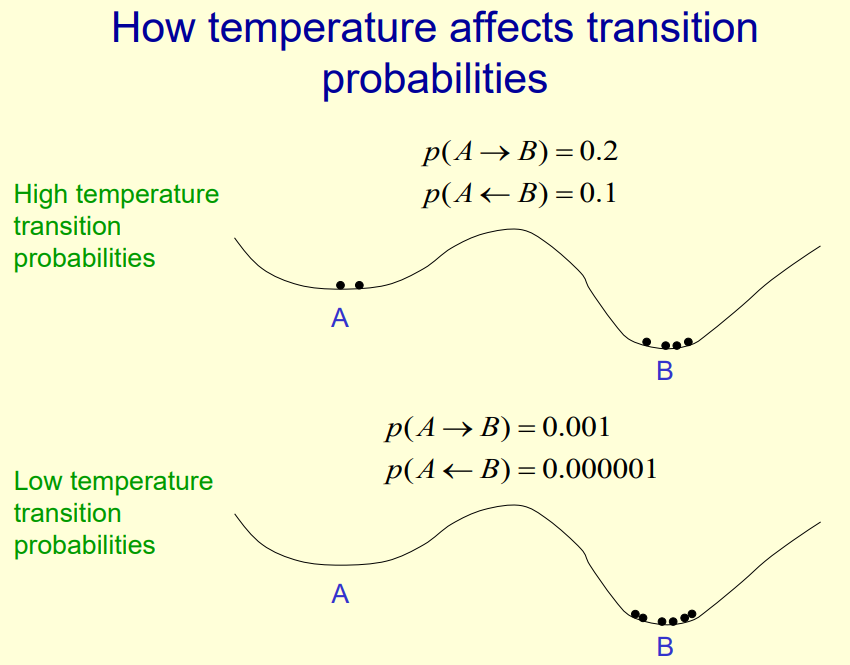
As long as there is some temperature/noise - if we run it long enough - all particles will eventually end up at B. But at low temperature this may take ages.
That’s why we start high and gradually reduce.
References
optimization
energy-based models