Introduction to RL

This note is mostly from long ago, so for a higher quality intro, refer to https://lilianweng.github.io/posts/2018-02-19-rl-overview/ or steve brunton’s playlist (this note is not based on these) or the various, newer, topical notes. Though this does cover some basics which I don’t mention in any other note. I also shifted some stuff to RL.

---

An agent learns and takes actions at each moment in time: $A_t$.
The action is received by the environment which gives a reward and state at the next moment in time ($R_{t+1},S_{t+1}$) → Passed back to agent to decide next acition.

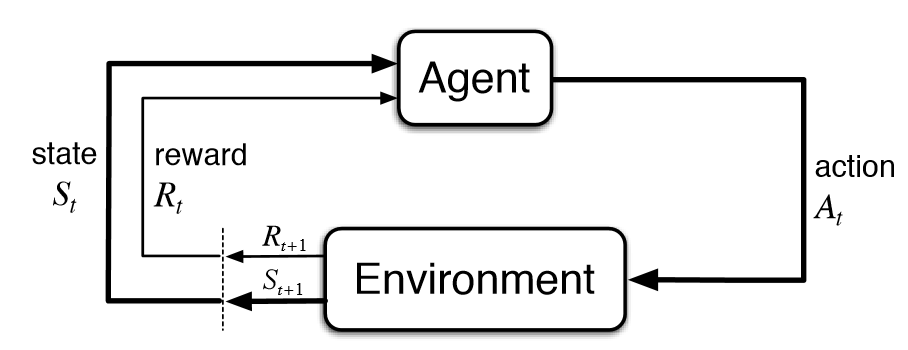
$S,A,R$ form a Finite Markov Decision Process.

Note

Uppercase indicates random variabes.
Lowercase indicates values they can take.

$t\in \{0,1,2,\dots \}$ (=discrete)
$s\in \mathcal{S}$ (finite set of anything)
$a\in \mathcal{A}(s)$ (set of actions we can take depends on the state we are in)
$r\in \mathcal{R}\in \mathbb{R}$ (finite subset of real number line; e.g. $r\in \{-1,0,1\}$)

$s$ is a complete description of the “world”, while and observation $o$ is a partial description of a state.

The dynamics of the agent / env interaction is specified by this distribution function

$$\text{displaylines}\begin{array}{r}\underset{\text{shorthand}}{\underbrace{p(s^{\prime },r|s,a)}}=\text{Prob}(S_{t+1}=s^{\prime },R_{t+1}=r|S_t=s,A_t=a)\end{array}$$

… gives the probability of the next state and reward, given the current state and some action to be taken.

Transclude of markov-property#^00e0f6

The agents behaviour is given by the policy:

$$\text{displaylines}\begin{array}{r}{a}_t\sim \pi (a|s)\end{array}$$

The policy gives the probability distribution over actions in a given state.
The agent samples randomly from this distribution (=stochastic).
If only one action can be taken from each state, the policy is deterministic:

$$\text{displaylines}\begin{array}{r}{a}_t=\pi (s)\text{or}{a}_t=\mu (s)\end{array}$$

In deep RL, the parameters of the network are also mentioned in the notation

$$\text{displaylines}\begin{array}{rl}{a}_t& ={\mu }_{\theta }(s_t)\\ a_t& \sim {\pi }_{\theta }(\cdot |s_t).\end{array}$$

This means the action at time $t$ is determined by applying the policy $\mu$ or $\pi$, which is determined by the weights of the network $\theta$.

Action spaces are the set of actions an agent can take. They can be either discrete (like in chess) or continous (robots in the real world) → real-valued vectors.
Not all deep RL methods work for both cases.

A trajectory $\tau$ is a sequence of states and actions in the world:

$$\tau =(s_0,a_0,s_1,a_1,\dots )$$

(also called episode or rollout)

The very first state of the world $s_0$ is randomly sampled from the start-state distribution, sometimes denoted by ${\rho }_0$:

$$s_0\sim {\rho }_0(\cdot ).$$

In normal chess, $s_0$ is deterministc.
State transitions can be either deterministic,

$$\text{displaylines}\begin{array}{r}{s}_{t+1}=f(s_t,a_t)\end{array}$$

or stochastic,

$$\text{displaylines}\begin{array}{r}{s}_{t+1}\sim P(\cdot |s_t,a_t)\end{array}$$

The reward depends on the current and next state and the action taken:

$$\text{displaylines}\begin{array}{r}{r}_t=R(s_t,a_t,s_{t+1})\end{array}$$

Frequently it is simplified to just depend to the dependence on the current state, $r_t=R(s_t)$, or state-action pair, $r_t=R(s_t,a_t)$.

The goal of the agent is to maximize some notion of cumulative reward (return) over a trajectory, but this can actually mean a few things.
The simplest kind of return is the finite-horizon undiscounted return:

$$\text{displaylines}\begin{array}{r}R(\tau )=\sum _{t=0}^T{r}_t\end{array}$$

… the sum of rewards in a fixed window of steps.

The infinite-horizon discounted return is the sum of all rewards ever obtained by the agent, but rewards are discounted by how far off in the future they are obtained:

$$\text{displaylines}\begin{array}{r}R(\tau )=\sum _{t=0}^{T=\infty }{\gamma }^t{r}_t\end{array}$$

Smaller $\gamma ⇝$ early rewards are more important.
Intuitively, it is better to have rewards right away than having to wait for them.
Mathematical reason: An infinite-horizon sum of rewards may not converge to a finite value (could just get higher and higher) → hard to deal with in equations. With $\gamma$, the infinite sum converges.

Note

While the line between these two formulations of return are quite stark in RL formalism, deep RL practice tends to blur the line a fair bit—for instance, we frequently set up algorithms to optimize the undiscounted return, but use discount factors in estimating value functions.

So our goal is to maxmize the expected return. For that, we need the probability of the different trajectories.
In the case of a stochastic policy and environment, the probability(distribution) of a $T$-step long trajectory (state action sequence) under a given policy look like this:

$$\text{displaylines}\begin{array}{r}P(\tau |\pi )={\rho }_0(s_0)\prod _{t=0}^{T-1}P(s_{t+1}|s_t,a_t)\pi (a_t|s_t).\end{array}$$

… multiply the initial state distribution with the sequence of distributions over actions and states.
Then the exptected return (for whichever measure) is:

$$\text{displaylines}\begin{array}{r}J(\pi )={\int }_{\tau }P(\tau |\pi )R(\tau )=\underset{\tau \sim \pi }{\mathbb{E}}[R(\tau )]\end{array}$$

… we sum over the probability of all possible trajectories times the respective reward (integral due to continous case).
In practice, we can’t calculate all trajectories, so we sample a subset from $\pi$. That’s also where Monte Carlo methods come into play.

The central optimization problem in RL can then be expressed by:

$$\text{displaylines}\begin{array}{r}{\pi }^{\ast }=\arg \underset{\pi }{\max }J(\pi )\end{array}$$

${\pi }^{\ast }$ … optimal policy
$\underset{\pi }{\mathrm{argmax}}$ … for which policy $\pi$ does $J(\pi )$ achieve the highest value? The $\arg \max$ returns the actual policy, rather than the max value itself.
We end up with the policy of the highest average return.

Value Functions tell us the complete future value (expected return) of a state / state action pair, provided that we act according to a particular policy forever after. They are used in almost every RL algorithm.

On-Policy Value Function (a state value function):

$$\text{displaylines}\begin{array}{r}{V}_{\pi }(s)=\underset{\tau \sim \pi }{\mathbb{E}}[R(\tau )|s_0=s]\end{array}$$

… gives the expectation of the return, given the agent starts at state $s$ and always acts according to the policy $\pi$ afterwards.
Same as the goal function, the thing we optimize for, but broken down by state. $V$ tells us how good it is to be in some state.

Breaking it down even further with the On-Policy Action-Value Function:

$$\text{displaylines}\begin{array}{r}{Q}_{\pi }(s,a)=\underset{\tau \sim \pi }{\mathbb{E}}[R(\tau )|s_0=s,a_0=a]\end{array}$$

… expectation of the return, given the agent starts at state $s$, takes an arbitrary action action $a$ (doesn’t need to be from the policy), and
always follows the policy $\pi$ afterwards. $Q$ tells us which action to take.

With these two functions we want to find the optimal policy ${\pi }_{\star }$.
A policy is optimal, if it achieves the highest possible expected return for all states:

$$\text{displaylines}\begin{array}{rlr}{V}_{{\pi }_{\star }}(s)& \ge V_{\pi }(s)& \text{for all}s\text{and for any}\pi \\ Q_{{\pi }_{\star }}(s,a)& \ge Q_{\pi }(s,a)& \text{for all}s,a\text{and for any}\pi \end{array}$$

There is always at least one optimal policy.
Abbrev. notation for optimal policies: $V_{\star }(s)$ or $Q_{\star }(s,a)$.

Dynamic Programming

Refers to algorithms used to find optimal policies which have complete knowledge of the environment as an Markov decision process → The dynamic program has access to: $p(s^{\prime }r|s,a)$

Another way of formulating it is by writing down the Optimal Value Function and the Optimal Action-Value Function:

$$\text{displaylines}\begin{array}{rl}{V}_{\ast }(s)& =\underset{\pi }{\max }\underset{\tau \sim \pi }{E}[R(\tau )|s_0=s]\\ Q_{\ast }(s,a)& =\underset{\pi }{\max }\underset{\tau \sim \pi }{E}[R(\tau )|s_0=s,a_0=a]\end{array}$$

… we start at state $s$ (+ take action $a$) and then act according to the optimal policy forever after.

The optimal policy gives us the optimal action:

$$\text{displaylines}\begin{array}{r}{a}_{\ast }(s)=\arg \underset{a}{\max }{Q}_{\ast }(s,a)\end{array}$$

There may be multiple actions that maximize the return but there is also always one which deterministically selects the optimal action.

The $Q$ and the $V$ function don’t just look simmilar, they also have a nice relation to eachother:

$$V^{\pi }(s)={\mathbb{E}}_{a\sim \pi }[Q^{\pi }(s,a)]$$

… the value of a state if you act according to a policy is the average / expected action value of that policy in that state.

$$V^{\ast }(s)=\underset{a}{\max }{Q}^{\ast }(s,a)$$

… the optimal value of a state is the maximum action value that can be optained from a state.

Bellman Equations / Q-learning

What the $Q/V$ functions tell us, are not just the immediate reward that I get in the state or the immediate reward following an action, but the likelihood of ending up in a good / bad state after taking some action / being in some state is also accounted for.
So the reward is the reward I get right now (might be nothing until the terminal state like in chess, or might be huge even though end-goal is not reached) and the sum of the following rewards (=return), following $\pi$ recursively, discounted:

$$\text{displaylines}\begin{array}{r}{Q}_{\pi }(s,a)=\underset{\text{no}\pi }{\underbrace{r(s,a)}}+\underset{\text{no}a}{\underbrace{\sum \gamma \cdot r(s^{\prime },\pi (s^{\prime }))}}\end{array}$$

The basic idea of the Bellman Equation is:
If the $Q$ function can give me an estimate of the reward for a function, why don’t I always ask it, rather than the policy? →

$$\text{displaylines}\begin{array}{r}{\pi }_Q(s)=\underset{a}{\max }{Q}_{{\pi }_Q}(s,a)\end{array}$$

Here is where the recursion comes into play:

What shall I do right now, If I also intend to follow this function in the future.

More formal way of noting down the Bellman Equations:

$$\text{displaylines}\begin{array}{rl}{V}_{\pi }(s)& =\underset{s^{\prime }\sim P}{\underset{a\sim \pi }{\mathbb{E}}}\left[r(s,a)+\gamma V_{\pi }(s^{\prime })\right]\\ Q_{\pi }(s,a)& =\underset{s^{\prime }\sim P}{\mathbb{E}}\left[r(s,a)+\gamma \underset{a^{\prime }\sim \pi }{\mathbb{E}}[Q_{\pi }(s^{\prime },a^{\prime })]\right]\end{array}$$

where $s^{\prime }\sim P$ is shorthand for $s^{\prime }\sim P(\cdot |s,a)$, indicating that the next state $s^{\prime }$ is sampled from the environment’s transition rules; $a\sim \pi$ is shorthand for $a\sim \pi (\cdot |s)$; and $a^{\prime }\sim \pi$ is shorthand for $a^{\prime }\sim \pi (\cdot |s^{\prime })$.

Now we know that the $Q$ function tells us what a good state is, and that we can use it as our policy, but how do we learn a good $Q$ function?

We start off with with a $Q$ function (neural net with parameters $\theta$), that doesn’t know anything about what a good state is or not, it has a random estimate of the reward.

$$\text{displaylines}\begin{array}{r}{Q}_{\theta }(s,a)=\tilde{R}\end{array}$$

This neural network then maps from the input state to a distribution over actions (in the discrete case).
It can also encode the action as input and then have just a single output. This has some drawbacks however, like having to do a separate forward pass for each action → cost scales linearly with the number of actions.

The total current reward of the net is the actual reward at the current step + the estimated reward for the future (sloppy notation):

$$\text{displaylines}\begin{array}{r}{Q}_{\theta }(s)=r_t+Q_{\theta }(s^{\prime })\end{array}$$

Or we can rearrange to: $$
\displaylines{\begin{align}
r_t = Q_\theta(s) - Q_
\underset{
\text{fixed}
}{
\theta
}
(s’)
\end{align}}

So the reward for any step is the difference between the Q-function of this and the next step. Q-learning is thus a form of [[temporal difference learning]]. We have a fixed set of predictions, which we update every $n>1$ steps (for stability reasons) with the weights of a second net which learns from new experiences. In short: The model improves by going through episodes (irl randomly sampled experiences from episodes) and **comparing** its **reward estimates with the actual rewards** $\theta$ was temed a [[DQN|Deep Q Network]] in the Atari paper which kickstarted Deepmind in 2013. ^a06a7d The delayed update of the target network might seem counter-intuitive but it has advantages of: - Stabilizing the training by reducing the variance in gradient updates - Improving generalization trough preventing overfitting on recent experiences The update can be *hard* by replacing the target weights by the policy weights or it could be *soft*, continously nudging the target weights by some factor. ## References Some sources https://spinningup.openai.com/en/latest/spinningup/rl_intro.html https://youtu.be/NFo9v_yKQXA?list=PLzvYlJMoZ02Dxtwe-MmH4nOB5jYlMGBjr [short TD Medium article](https://towardsdatascience.com/introduction-to-reinforcement-learning-rl-part-6-temporal-difference-td-learning-2a12f0aba9f9) [[probability]] [[reinforcement learning]]