convergence

Convergence

We say that the sequence $(a_n{)}_{n\in \mathbb{N}}\subseteq \mathbb{C}$ converges to $a$ iff:

$$\begin{array}{rl}& \forall \epsilon >0\exists n_0\in \mathbb{N}\forall n\ge n_0:|a_n-a|<\epsilon \\ ⟺& \forall e>0\exists n_0\in \mathbb{N}\forall n\ge n_0:a_n\in U_{\epsilon }(a)\\ ⟺& \forall \epsilon >0\exists n_0\in \mathbb{N}:(a_n{)}_{n=n_0}^{\infty }\subseteq U_{\epsilon }(a)\end{array}$$

where $U_{\epsilon }(a)$ is the epsilon neighbourhood of $a$.
We then call $a$ the limit of the sequence and write:

$$\underset{n\to \infty }{\lim }{a}_n=a\text{or simply}{a}_n\to a$$

The sequence is called convergent, or we say that its limit exists, if such an $a$ exists. Otherwise, the sequence is called divergent.

The limit does not depend on the finite number of initial terms.

If $(b_n)$ is a sequence with $b_n=a_n$ for almost all $n$, i.e. there exists $n_0$ such that $b_n=a_n$ for all $n\ge n_0$, then $a_n\to a⟺b_n\to a$.

Convergence means oscillations must die out

The definition demands: for any $\epsilon$ (no matter how small), eventually the sequence stays within that $\epsilon$-ball forever. This is stricter than boundedness. A sequence can be bounded yet divergent if it keeps jumping around.

Complex convergence

For $(z_n)\subset \mathbb{C}$ with $z=x+iy$:

$$z_n\to z⟺\mathrm{Re}{z}_n\to x\text{ and }\mathrm{Im}{z}_n\to y$$

$a_n=\frac{1}{n}\to 0$

For any $\epsilon >0$, the archimedean property gives $n_0\in \mathbb{N}$ with $\frac{1}{n_0}<\epsilon$.
Then for $n\ge n_0$: $|a_n-0|=\frac{1}{n}\le \frac{1}{n_0}<\epsilon$.

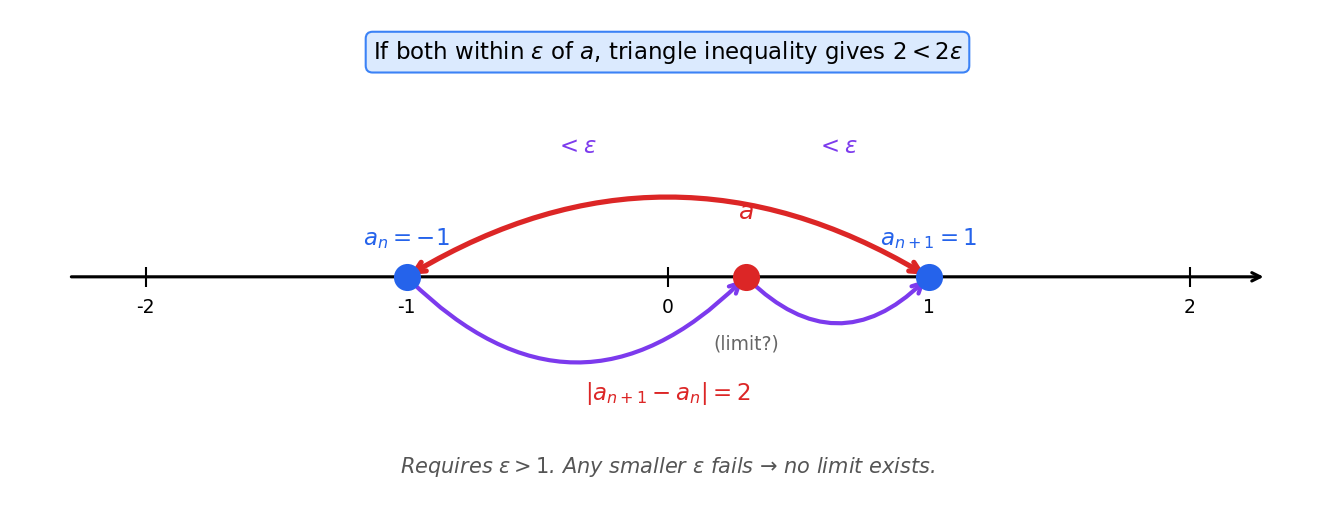
$a_n=(-1{)}^n$ is divergent

Proof by contradiction: suppose $a_n\to a$ for some $a\in \mathbb{R}$.

Pick $\epsilon =\frac{1}{2}$. By convergence, there exists $n_0$ with $a_n\in U_{1/2}(a)$ for all $n\ge n_0$.

But consecutive terms satisfy $|a_{n+1}-a_n|=2>1$, so they can’t both lie in a ball of radius $\frac{1}{2}$. Contradiction.

Any $\epsilon <1$ works. If both $a_n,a_{n+1}\in U_{\epsilon }(a)$, the triangle inequality gives:

$$|a_{n+1}-a_n|=|(a_{n+1}-a)+(a-a_n)|\le |a_{n+1}-a|+|a_n-a|<2\epsilon$$

But $|a_{n+1}-a_n|=2$, so we need $2\epsilon >2$, i.e. $\epsilon >1$.

Definite divergence (improper limits)

Let $(a_n{)}_{n\in \mathbb{N}}\subset \mathbb{R}$. The sequence tends to $\infty$ (or $+\infty$) if

$$\forall A>0\exists n_0\in \mathbb{N}\forall n\ge n_0:a_n>A$$

We write $a_n\to \infty$ or ${\lim }_{n\to \infty }{a}_n=\infty$, and call $\infty$ the improper limit.
Tendency to $-\infty$ is defined analogously with $a_n<-A$.

If a sequence tends to $\pm \infty$, it is called definitely divergent.

Definitely divergent sequences are necessarily unbounded (no finite bound can contain all terms). They can still be bounded from one side: $a_n=n$ diverges to $+\infty$ but is bounded below.

This concept only applies to real-valued sequences. Complex numbers have no compatible order, so “tending to infinity” in $\mathbb{C}$ isn’t defined this way.

Limit arithmetic

Let $(a_n),(b_n)$ be convergent sequences with $a:={\lim }_{n\to \infty }{a}_n$ and $b:={\lim }_{n\to \infty }{b}_n$, and let $\lambda \in \mathbb{C}$. Then:

$$\begin{array}{rl}\underset{n\to \infty }{\lim }(a_n+b_n)& =a+b\\ \underset{n\to \infty }{\lim }(\lambda \cdot a_n)& =\lambda \cdot a\\ \underset{n\to \infty }{\lim }(a_n\cdot b_n)& =a\cdot b\\ \underset{n\to \infty }{\lim }\frac{a_n}{b_n}& =\frac{a}{b}\text{if }b\ne 0\end{array}$$

The same rules hold for function limits ${\lim }_{x\to c}f(x)$.

Link to original

Sandwich rule

Let $(a_n),(b_n),(c_n)\subset \mathbb{R}$ be sequences with

$$a_n\le b_n\le c_n\text{for all }n\in \mathbb{N}$$

If $(a_n)$ and $(c_n)$ converge to the same limit $a$, then $(b_n)$ also converges to $a$:

$$\underset{n\to \infty }{\lim }{a}_n=\underset{n\to \infty }{\lim }{c}_n=a⟹\underset{n\to \infty }{\lim }{b}_n=a$$

Link to original