projection

A projection is a kind of linear transformation.

Matrix multiplication can project one vector space onto a different subspace: ${\mathbb{R}}^{m\times n}\mapsto {\mathbb{R}}^{m\times p}$

Projections onto lower-dimensional subspaces are not invertible / surjective – there is a loss of information.

Projection

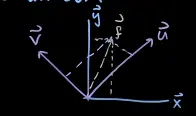
The same vector $\mathbf{f}$ can be viewed from the perspective of different basis vectors.

The projection $\mathbf{f}$ onto a line $\text{span}\{\mathbf{v}\}$ is the foot (closest point) of the perpendicular (dashed lines) from $\mathbf{f}$ to that line. If the basis vectors are orthogonal, the coefficients can be computed with inner products:
Let $\hat{v}=v/\Vert v\Vert$ be a unit vector in the direction of $v$, then the projection onto a single direction is:

$${\text{proj}}_{\hat{v}}(\mathbf{f})=⟨\mathbf{f},\hat{v}⟩\hat{v}=(\mathbf{f}\cdot \frac{v}{\Vert v\Vert })\frac{v}{\Vert v\Vert }=\frac{⟨\mathbf{f},v⟩}{\Vert v{\Vert }^2}v$$

This way, we can write $\mathbf{f}$ as a linear combintation of orthogonal basis vectors $\mathbf{x},\mathbf{y}$ or $\mathbf{u},\mathbf{v}$:

$$\mathbf{f}=\frac{⟨\mathbf{f},\mathbf{x}⟩}{\Vert \mathbf{x}{\Vert }^2}\mathbf{x}+\frac{⟨\mathbf{f},\mathbf{y}⟩}{\Vert \mathbf{y}{\Vert }^2}\mathbf{y}\mathbf{f}=\frac{⟨\mathbf{f},\mathbf{u}⟩}{\Vert \mathbf{u}{\Vert }^2}\mathbf{u}+\frac{⟨\mathbf{f},\mathbf{v}⟩}{\Vert \mathbf{v}{\Vert }^2}\mathbf{v}$$

The projection is idempotent: Applying it twice is the same as applying it once:

References

Visualization of different matrices