linear transformation

Linear vs Affine

A linear transformation is a special case of an affine transformation, which can include translations (shifts).

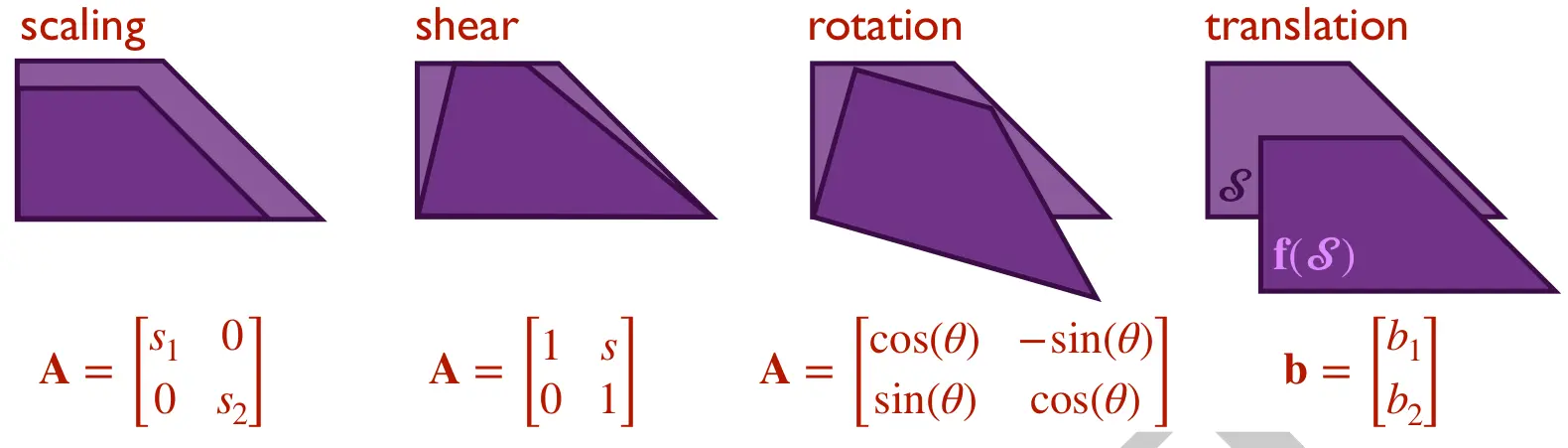
Visualization of different transformation matrices

The columns of a linear transformation matrix tell you where the basis vectors are going to end up after the transformation.

However, a better way is to find out is by computing the eigenvalues / eigenvectors.

See also geometric projection.

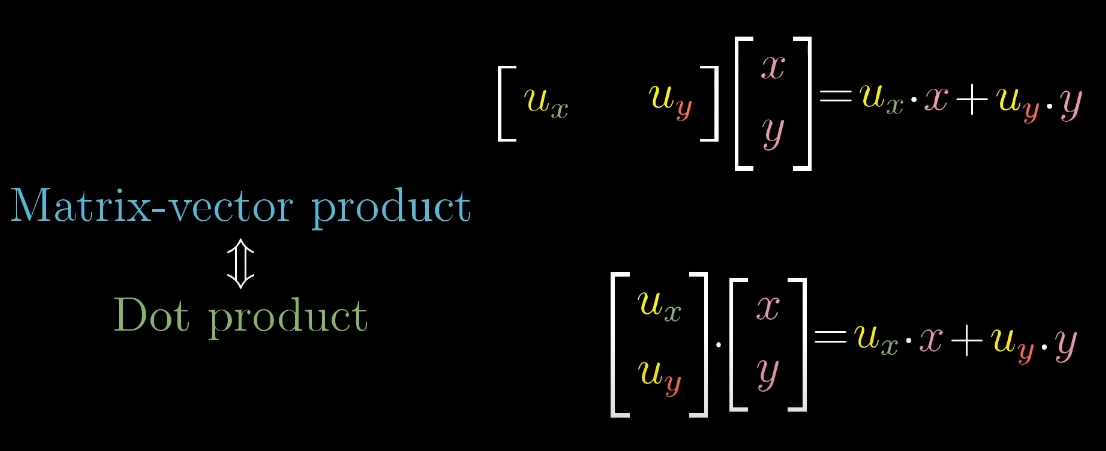
Matrix Vector Product Intuition

Linear Transformations onto a number line can be interpreted as taking the dot product with a unique vector $\vec{v}$ that corresponds to that transformation.

Projecting a vector onto the span of the unit vector:

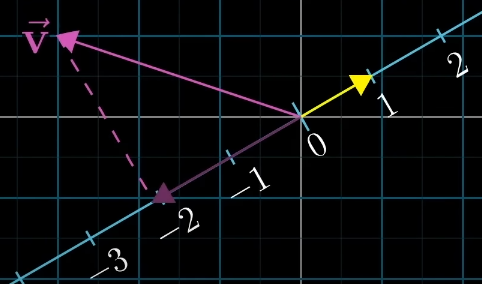
That vector really is just shorthand for what happens if we squish all that space onto it / project the unit vectors onto it → Think through why red is longer than green in that example and you’ll see.

---

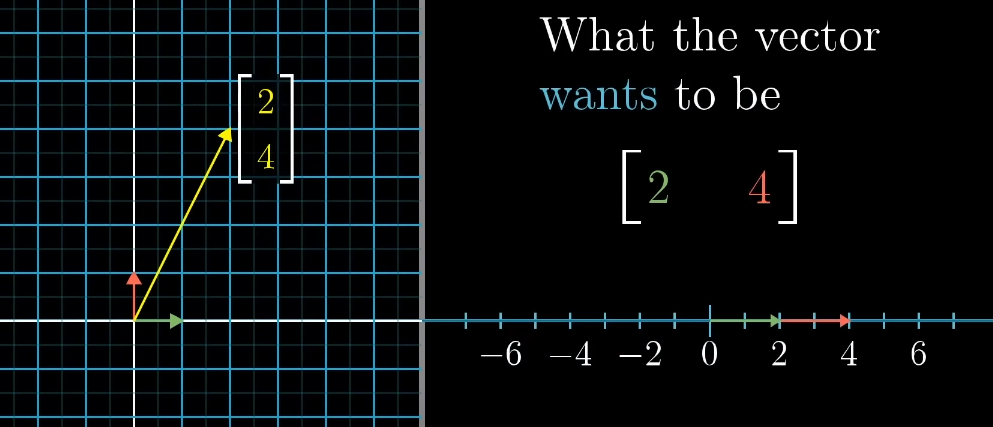
Linear transformation matrix $m=\left[\begin{array}{cc}2& 4\end{array}\right]$

$$\begin{gathered} \text{displaylines}\hat{i}=\left[\begin{array}{cc}1& 0\end{array}\right] \\ \hat{j}=\left[\begin{array}{cc}0& 1\end{array}\right] \\ m\cdot \hat{i}=2 \\ m\cdot \hat{j}=4 \end{gathered}$$

---