surprise

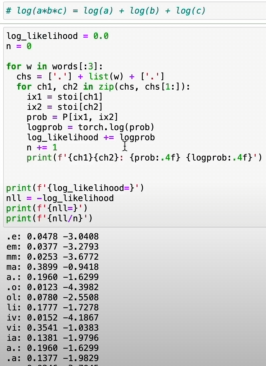
Shannon information / Self-information / Surprise

$$I(x)=log(\frac{1}{p(x)})=\log (1)-\log (p(x))=-\log p(x)$$

The base of the logarithm sets the units. With $b=2$, we measure in bits.

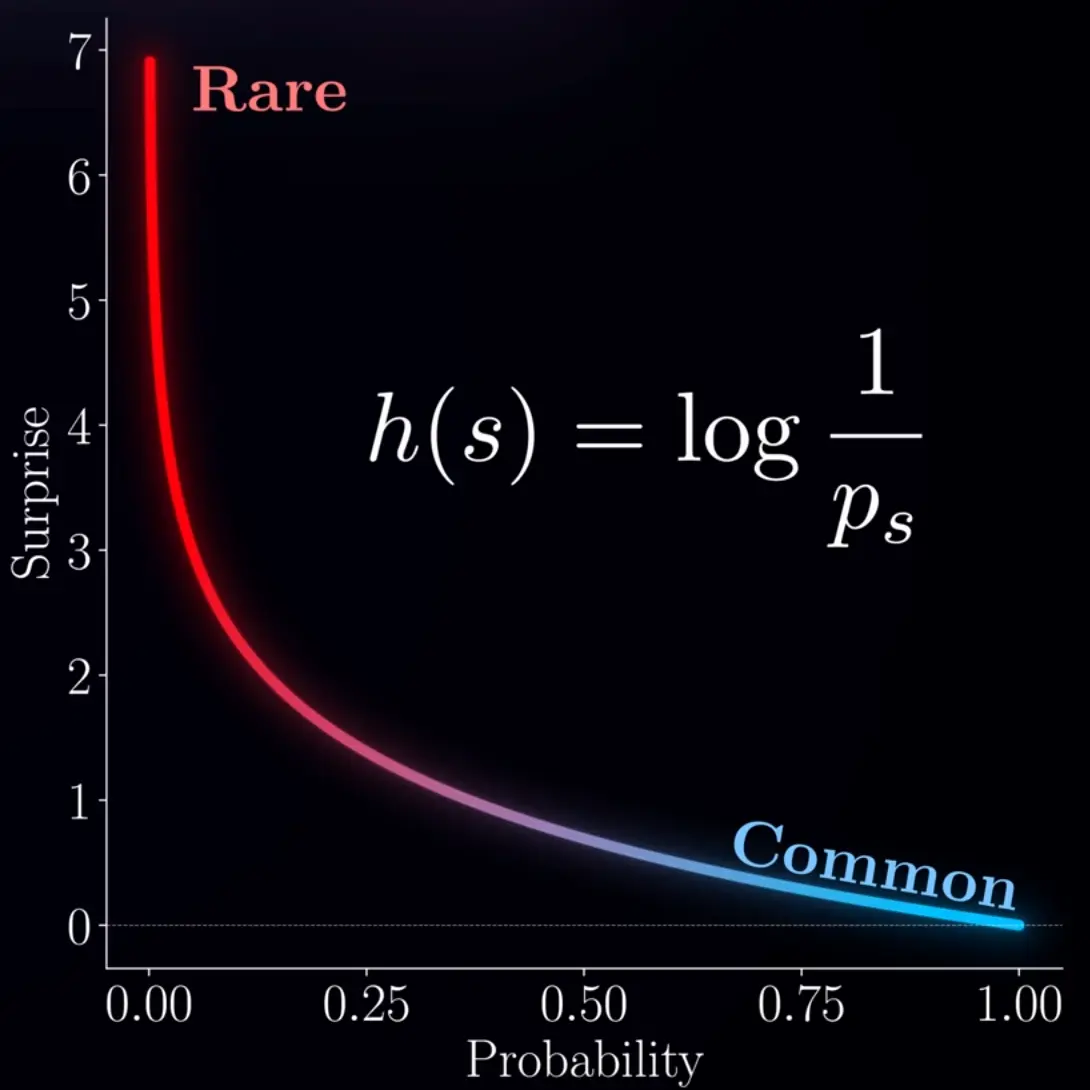
(s is the state in the above image, h is the surprise function)

Extreme cases:
p(x) = 1 → 0 surprise
p(x) = 0 → $\infty$ surprise
Information content with bits:
p(x) = 1/2 → 1 bit
p(x) = 1/4 → 2 bits
p(x) = 1/8 → 3 bits
p(x) = 1/10 → ~3.32 bits
p(x) = 1/100 → ~6.64 bits

The expected value of surprise is entropy:

Entropy (Information Theory)

Entropy is the expected value of surprise/self-information of a discrete random variable $X\sim P$:

$$H(P)=\mathbb{E}[I(X)]=-\mathbb{E}[\log (p(X))]=-\sum _{x\in X}p(x)\log (p(x))$$

Note: The continuous form $\int p(x)\log (p(x))dx$ “differential entropy” is not analogous and not a good measure for uncertainty or information, as it can be negative (even infinite), and is not invariant under continuous coordinate transformations. See wikipedia.

Link to original

Additivity of information

Two independent probabilities multiply, the information of two independent events should add, intuitively.
The logarithmturns multiplication into addition:

$$\begin{array}{rl}P(A\cap B)& =P(A)\cdot P(B)\\ I(A\cap B)& =I(A)+I(B)\end{array}$$

$P$ and $Q$ are not interchangable

$$H(P,Q)\ne H(Q,P)$$

E.g.: If you believe a coin is fair (0.5/0.5), but it is rigged (0.99/0.01), then the CE is: $0.99\log \left(\frac{1}{0.5}\right)+0.01\log (\frac{1}{0.5})\approx 0.7$
If you believe it is rigged when it is actually fair, then the CE is: $0.5\log \left(\frac{1}{0.99}\right)+0.5\log (\frac{1}{0.01})\approx 2.4$
In the second case, the entropy is much larger, as half of the time you are extremely surprsied to see tails, this extreme surprise dominates the average surprise.

Link to original

More surprising things are harder to compress.
In machine learning, for example if we predict how likely a football team is to win, we want to achieve a very low suprise (loss), so we can estimate confidently:

In machine learning, we want the next target to have a very high probability, i.e. low surprise → negative log-likelihood loss

Don’t get confused

Quantity	Formula	Depends on
Surprise / self-information	$I_p(x)=-\log p(x)$	$p$
Per-example NLL (log-likelihood)	$-\log p_{\theta }(x)$	$\theta$
cross-entropy $H(q,p_{\theta })$	${\mathbb{E}}_q[-\log p_{\theta }(X)]$	$\theta$, $q$

References

The Key Equation Behind Probability