ResNet

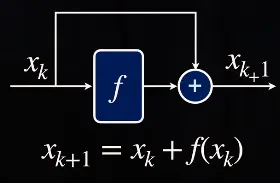
motivation / intuition

Learning $y=x+f(x)$ is easier than learning $y=f(x)$
Instead of learning the mapping $x\mapsto y$, we only learn the small difference / “residual”.

To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.

• Most of the time, the input will be close to the output (think resolution upscaling task).
• The network does not need to worry about memorizing the input.
• Vanishing gradients are prevented

This also guarantees, in terms or representational power, that a bigger network can at least perform as well as a smaller one, in theory: https://d2l.ai/chapter_convolutional-modern/resnet.html#function-classes (${\mathcal{F}}_L\subset {\mathcal{F}}_{L+1}$).

Classic resnet block, size is preserved:

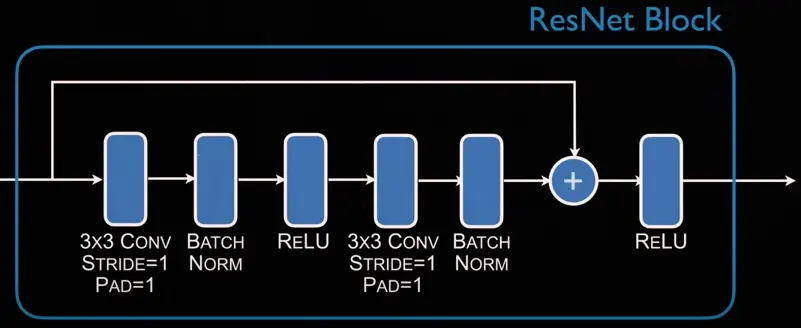
Increasing the stride (and proportionally also the conv channels) reduces the spatial dim and is often done in classification.

Resnet is a discrete, less general case of NODEs, it is an euler integrator, but there are much better ones:
See overview and intuition

Other types of skip connection.

References

Official pytorch code
Residual Connection | PapersWithCode